Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями, правило, примеры для тренировки

Деление в столбик – правила

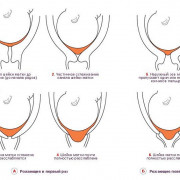
Для того, чтобы уметь делить в столбик необходимо знать некоторые правила. Именно об этом и пойдет далее речь. Ведь деление в столбик невозможно освоить если не знать элементарного – таблицы умножения. Считать простые примеры на умножение необходимо быстро и в уме. Это только в начале обычно дети пользуются черновиками, чтобы подобрать множитель, таким образом найти частное. Еще надобно уметь разбивать числа на сотни, десятки, тысячи – не путаться и в этих понятиях. Для наглядности, где делимое, где делитель, где частное можете изучить термины на изображении ниже.

Что нужно знать для деления в столбик?

Прежде, чем приступать к делению, следует проверить ребенка на знания элементарных правил. Ведь пропускать математику нельзя. А если пропуски все же были, то нужно изучить тот материал, что изучали ранее на уроках в школе

Понадобится обратить внимание на такие знания, как:

Запомнил ли школьник, как называются все элементы, участвующие в процессе деления.

Обратите внимание на знание таблицы умножения ребенком.
Еще ребенок должен усвоить, какие бывают разряды числа (единицы, десятки, сотни).

Пример: 

1. 57: 3, где 57 – это делимое, число, что разделяют на доли, а 3 – это делитель, указывающий, на сколько делить предыдущее число.
2. Определяемся, вначале какие единицы выделить в делимом для осуществления деления в столбик числа 57. Число 5 > 3.
3. Узнайте, сколько раз следует взять число 3, чтобы получить 5. Результат 3 · 1 = 3 ≤ 5. Значит подходит и 1 поставьте в качестве первой цифры частного.
4. Теперь вычитание: 5 — 3 = 2. Остаток 2 и единицу сносим, выходит 27.
5. Находим теперь, на какое число нужно умножить 3, чтобы результат был 27. Согласно таблице умножения 3 · 9 = 27.
6. Итого результат 19.

Умножение, деление – взаимосвязаны между собой, хотя и противоположные операции. Чтобы проверить, верно ли нашли частное, необходимо выполнить умножение. Потому таблица умножения и умение умножать на черновике без калькулятора всегда пригодится ребенку, также еще при умножении следует уметь правильно прибавлять, а при делении в столбик вычитать. В математики все действия с числами между собой взаимосвязаны.

Ниже смотрите пример деления в столбик 536 на 4. Действия с трехзначным делимым выполняются аналогично, что и с двухзначным.

Деление

Деление в школе начинают учить уже с третьего класса. Школьники только изучают азы процесса, выполняют самые простые примеры на это действие.

Примеры подобны умножению, только детей учат таблице деления, а не умножения. Школьники должны уловить саму суть, что означает поделить число на несколько частей, изучают, что такое делимое, делитель, частное. Узнают, как проверить умножением правильность решения примера или же задачи. В столбик дети еще не считают, так как даются самые простые примеры и все числа из таблицы умножения. Пример: 81 : 9 = 9.

Процесс деления в четвертом классе значительно усложняется. Детям дают вначале года вспомнить, что они учили в третьем классе, а далее уже начинают осваивать технику деления чисел в столбик. Именно за этот учебный год осваивают такие знания. Ниже приведен алгоритм решения примеров в столбик с подробным описанием процесса.

Здесь даже учтено то, что возможно будет остаток при делении, что число получится не цельным, а через запятую.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

1. «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
2. «Деление. Уровень 4. Рабочая тетрадь» от Kumon
3. «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является  усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей

Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода. Для того чтобы легко научить ребёнка операции деления нужно:

Для того чтобы легко научить ребёнка операции деления нужно:

• Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
• Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.

Как объяснить ребенку деление и научить делить столбиком?

дети-школьники тренируются делить числа столбиком

Во-первых, учтите ряд вводных факторов:

• ребёнок знает таблицу умножения
• хорошо разбирается и умеет применять на практике действия вычитания и сложения
• понимает разницу между целым и его составными элементами

Дальше акценты в ваших действиях выглядят так:

• поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
• объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
• превратите процесс в игру, придумайте историю про цифры и действие деления,
• подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
• первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:

• запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
• предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
• подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
• помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
• следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
• снова помогите с записью действия,
• продолжайте до момента, когда результат от разницы составит ноль. Это актуально только для деления чисел без остатка,
• закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.

Общие сведения

Любую математическую операцию можно осуществить в столбик. Деление не является исключением. Следует отметить, что оно бывает без остатка и с ним. Если выполняется операция первого типа, то необходимо знать признаки деления. Последними называются правила, по которым можно определить — делится ли число на другое без остатка. Однако во втором случае в конце вычислений получается определенное значение. Его математики называют остатком.

Деление такого типа широко применяет в языках программирования для создания различных условий. Если необходимо произвести деление в столбик на однозначное число без остатка, то нужно знать признаки делимости. Последние не нужны в том случае, когда следует осуществить деление с остатком трехзначного числа на однозначное. Следует отметить, что нужно различать терминологию. Не все люди знают основное различие между цифрами и числами. Первые применяются для образования вторых, то есть первые — набор знаков.

Основным требованием, необходимым для осуществления этой операции, является доскональное знание таблицы умножения. Без последней не обходится ни один урок, письменное отчетное задание или сдача экзамена. Операция деления применяется реже сложения, вычитания или умножения. Однако ее следует знать досконально и уметь производить вычисления не только при помощи калькулятора или компьютера, но и в ручном режиме.

Иногда ученики сталкиваются с непониманием материала, который не может объяснить доходчиво учитель для каждого индивидуально. Если у ребенка проблемы в какой-либо учебной четверти, то не стоит затягивать с решением проблемы. Родителям нужно разработать собственную систему обучения или воспользоваться уже готовой. Однако некоторые из них начинают кричать на ребенка, травмируя психику. Следует помнить, что он часто копирует поведение родителей. Когда они его приучают к эмоциональному решению проблем, тогда и вырастают неуверенные в себе молодые люди.

Следует помнить, что для изучения любой точной науки необходимо терпение. Сразу ничего не получалось даже у знаменитых математиков. Необходимо дома создать уютный уголок с тренажерами для тренировок по решению математических задач. Пусть это будет своеобразный офис для малыша. Ему необходимо помочь его оборудовать: распечатать необходимый математический материал и сделать хорошее освещение.

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

• Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
• Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
• Запишите под числом 35 число 32.
• Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Деление с остатком

Простые примеры для ребенка

На этом же примере можно продолжить:

• При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
• При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
• Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
• В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
• При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.

Описание

Программа «Задание на неделю 3 класс» формирует задачи и примеры, которые помогают закрепить ребенку все знания, полученные во третьем классе в течение года, а также подготовится к проверочной и контрольной работе.

На листе формата А4 формируется 13 заданий по математике. При этом задания даются в небольшом объеме, но с максимальным охватом всех типов примеров. Это позволяет детям быстро вспомнить материал 3 класса.

В каждую карточку входят следующие виды заданий:

• задание на повторение понятий «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность», «множитель», «произведение», «делимое», «делитель» и «частное» с вычислениями;
• примеры на сложение, вычитание, умножение и деление, в том числе: логические (вставить знаки для получения верного равенства),
• выражения на порядок действий (от пяти действий со скобками);
• примеры на умножение и деление разных типов: умножение и деление круглых чисел, внетабличное умножение и деление;
• примеры на деление с остатком с вычисление частного, уменьшаемого или вычитаемого;
• решение уравнений;
• задание на сравнение дробей (долей) и нахождение части от числа;
• задания на повторение единиц измерения длины, массы и времени;
• примеры в столбик: сложение трехзначных чисел, вычитание трехзначных чисел, умножение двухзначного числа на однозначное, умножение трехзначного числа на однозначное и двузначное, на однозначное число;
• примеры на нахождение сторон, периметра и площади квадрата и прямоугольника;
• простые задачи на движение: нахождение скорости, времени или расстояния.

Программа «Задание на неделю 3 класс» написана в Excel с помощью макросов. Данные генерируются случайным образом, что позволяет получить более тысячи вариантов заданий для 3 класса, карточки заданий не повторяются.

Для ознакомления с программой можно скачать изображение карточки, которая получилась с помощью программы. Для получения новой карточки математического диктанта достаточно скачать, нажать на кнопку и распечатать.

Другие программы, которые помогут закрепить навыки счета:

• Цепочки примеров в пределах 1000 (все действия)
• Числовые пирамиды большие (в пределах 50,100 и больше)
• Умножение и деление по типам (табличное, внетабличное, круглых чисел)
• Сложение и вычитание в столбик
• Умножение и деление в столбик
• Деление с остатком на число (с выбором уровня сложности)
• Порядок действий в пределах 1000 (все действия)
• Сложные примеры на порядок действий
• Выражения с именованными числами

Как научиться делить столбиком на двузначное

В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.

Для примера выполним действие: 144 : 24

Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.

Разделим 1035 на 23.

Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.

Алгоритм деления в столбик

Для этого алгоритма следует воспользоваться наглядным примером (рис. 1). Следует разделить 792 на 2. Первоначальное число является трехзначным и состоит единиц, десятков и сотен. Записывается операция в столбик, как показано на рисунке 1. Цифра «7» — первое неполное делимое. Вторым неполным называется делимое, полученное на втором цикле операции, а третьим — на третьем.

Рисунок 1. Графическое представление деления трехзначного числа в столбик.

Исходя из рисунка 1, можно составить алгоритм деления в столбик. Его можно применять не только для трехзначного, но и шестизначного, десятизначного и многозначного чисел. Единственное правило: количество цифр делимого должно быть больше, чем число знаков делителя. Алгоритм имеет такой вид:

1. Записать делимое и делитель.
2. Выделить первое неполное делимое (7): подобрать целое число (должно быть не больше I делимого), на которое следует умножить делитель для получения приблизительного значения первого (3, поскольку 3 * 2 = 6. Если взять 4, то 8 > 7).
3. Произвести умножение и вычесть со значения первого (7 — 6 = 1), записав остаток. Если последнего нет, то ничего переносить не нужно.
4. Взять II неполное делимое с учетом остатка (19).
5. Подобрать множитель: 2 * 9 = 18 < 19.
6. Произвести операцию вычитания с выделением остатка: 19 — 18 = 1.
7. С учетом остатка (1) взять III неполное делимое (2).
8. Подобрать множитель: 2 * 6 = 12.
9. В остатке 0. Следовательно, операция закончена.

Деление в столбик с остатком осуществляется по такому же алгоритму. Например, 793 на два делится только с остатком. Чтобы не повторять вычисления с самого начала, можно воспользоваться уже готовыми. Для этого необходимо вернуться в седьмой пункт предыдущего алгоритма:

1. Остаток (1) и III неполное делимое (3): 13.
2. Множитель равен 6: 2 * 6 = 12 < 13.
3. Остаток эквивалентен 1, но всего III неполных делителя. Операция выполнена с остатком 1.

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

В частном будет однозначное число. 

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

 Значение частного чисел 768 и 24 равно 32.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое  414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными (многозначными) числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.
2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Правила деления в столбик

Без остатка

Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.

Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:

1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.

2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.

Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.

3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица

Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления

Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.

4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.

Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.

5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.

На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.

С остатком

В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.

Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).

Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.