Деление натуральных чисел столбиком: правило, примеры

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

на доске решены примеры на деление столбиком трёх- и более значных чисел

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

алгоритм деления столбиком четырёхзначного числа

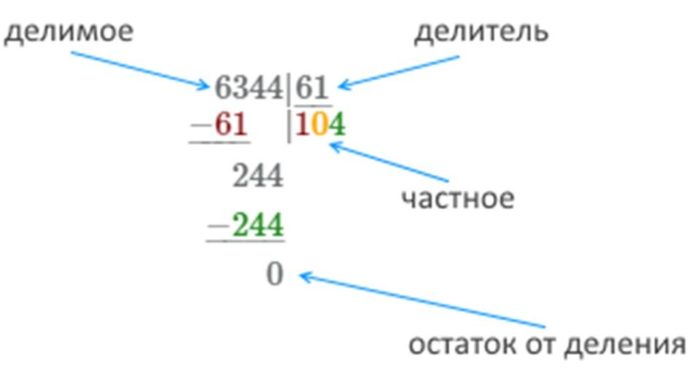
пример деления столбиком четырёхзначного числа на двузначное

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

Примеры подробного решения ниже.

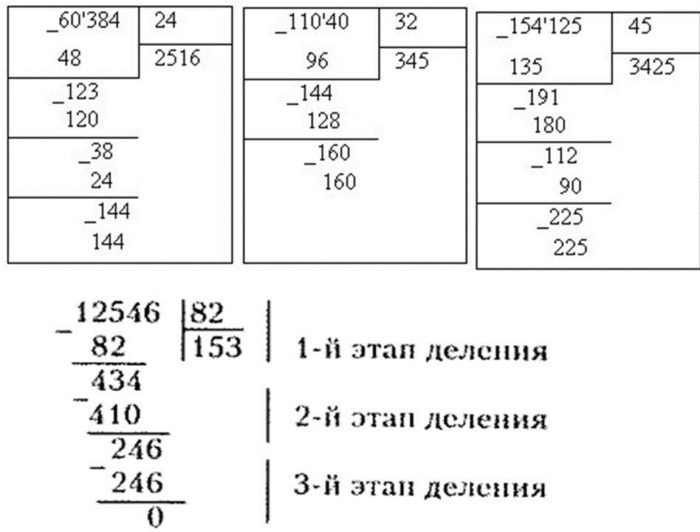
примеры деления столбиком многочленов

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

примеры деления многочленов в столбик

Как научиться делить столбиком трехзначные числа

Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.

Для примера рассмотрим следующие действия: 146676 : 719

146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.

1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».

Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

рисунок из презентации на тему деления трёхзначного числа столбиком

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

пример деления трехзначного числа на однозначное столбиком

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

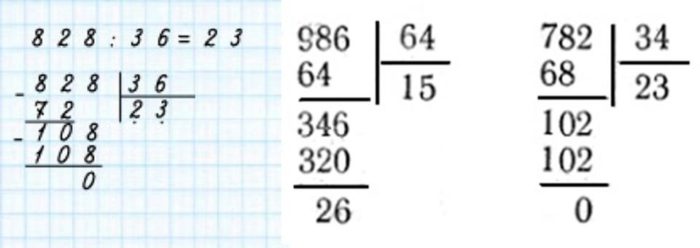
примеры деления столбиком трехзначных чисел на двузначные

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

пример деления в столбик трёхзначного числа на трёхзначное с остатком

Входная административная контрольная работа

1 вариант

1. Выполни вычисления

3 • 8 = 4 • 6 = 9 • 3 = 7 • 4 =

16 : 4 = 28 : 4 = 21 : 3 = 36 : 9 =

20 : 5 = 4 • 8 = 12 : 6 = 3 • 7 =

2. Вычисли

80 + 24 : 6 =

50 – 4 • (12 – 5) =

70 – 5 • 4 =

3. Задача

Упаковщица уложила в коробку 2 ряда синих кубиков, по 8 кубиков в ряду и 12 зелёных кубиков. Сколько всего кубиков было в коробке?

4. Реши уравнение

16 : х = 8                               6 • х = 12

5. Найди периметр прямоугольника, длины сторон которого 8 см и 6 см.

2 вариант

1. Выполни вычисления

3 • 9 = 7 • 3 = 3 • 4 = 4 • 6 =

36 : 4 = 20 : 5 = 18 : 6 = 28 : 7 =

7 • 2 = 8 • 4 = 27 : 9 = 2 • 8 =

2. Вычисли

70 + 5 • (12 – 8) =

12 : 6 + 6 • 3 =

60 + 3 • 8 =

3. Задача

Мама разложила пирожки на 3 маленькие тарелки, по 6 пирожков на каждую, и 10 пирожков на большую тарелку. Сколько всего пирожков на этих тарелках?

4. Реши уравнение

18 : х = 3                               7 • х = 14

5. Найди периметр прямоугольника, длины сторон которого 9 см и 5 см.

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, с нулями, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем и правил в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

Понравился наш контент? Подпишитесь на канал в .

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

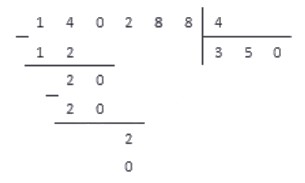
3. Выполняем операцию вычитания  и под чертой записываем результат.

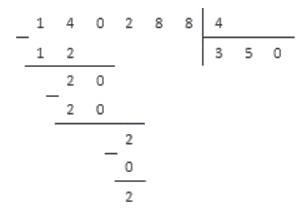
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

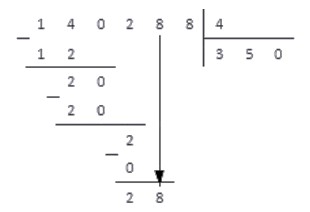
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

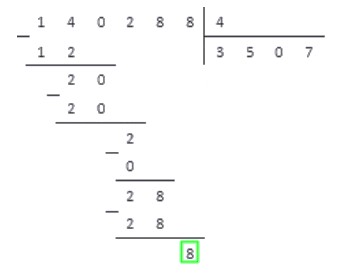
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

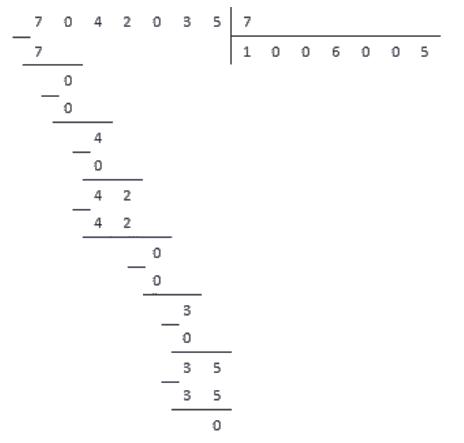
Ответ: 1006005

Обучение делению в столбик при помощи таблицы умножения

Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:

• Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
• Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
• Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.

Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.

Таблица умножения

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Деление многозначных чисел

Деление столбиком может показаться детям сложным, однако запомнить алгоритм несложно. Рассмотрим деление многозначных чисел на однозначное число:
215 : 5 = ?
Записывается вычисление следующим образом:
Под делителем будем записывать результат. Деление выполняется следующим образом: сравниваем крайнюю левую цифру делимого с делителем: 2 меньше 5, разделить 2 на 5 мы не можем, поэтому берем еще одну цифру: 21 больше 5, при делении получается: 20 : 5 = 4 (остаток 1)

Сносим к полученному остатку следующую цифру: получаем 15. 15 больше 5, делим: 15 : 5 = 3

Решение будет выглядеть таким образом:

Так производится деление без остатка. По тому же алгоритму производится деление в столбик с остатком с той лишь разницей, что в последней записи будет указан не ноль, а остаток.

Если необходимо произвести деление трехзначных чисел в столбик на двухзначное, порядок действий будет таким же, как при делении на однозначное число.

Приведем примеры на деление:

Аналогично проводится вычисление при делении многозначного числа на двузначное с остатком: 853 : 15 = 50 и ( 3 ) остатокОбратите внимание на эту запись: если при промежуточных вычислениях в результате получается 0, но пример не решен до конца, ноль не записывается, а сразу сносится следующая цифра, и вычисление производится дальше. Поможет усвоить правила деления многозначных чисел в столбик видеоурок

Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными

Поможет усвоить правила деления многозначных чисел в столбик видеоурок. Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными.

Важно! Следите за записью: разряды должны записываться под разрядами, в столбик. Видео «Деление в столбик»

Видео «Деление в столбик»

Если во 2 классе ребенок выучил таблицу умножения, примеры на умножение и деление двузначного или трехзначного числа на уроках математики за 4 класс не вызовет у него трудностей.

Читайте так же:

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

• Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
• Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
• Запишите под числом 35 число 32.
• Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Деление с остатком

Простые примеры для ребенка

На этом же примере можно продолжить:

• При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
• При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
• Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
• В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
• При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными (многозначными) числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.
2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Карточка 2

Сосчитай, записывая примеры в столбик.

32+49	37-16
46+24	70-48
83+8	53-38
38+32	45-8

Сосчитай, записывая примеры в столбик.

80-67	45+14
93-48	38+47
59-42	75+8
36-9	68+27

Сосчитай, записывая примеры в столбик.

46+37	80-38
22+58	93-56
59+9	75-9
64+27	87-32

Карточка 7

В летний лагерь приехали дети на двух автобусах. В первом автобусе было 46 детей, а во втором — на 8 детей меньше. Сколько всего детей приехало в школьный лагерь?

3∙7	2∙9	5∙3	9∙0
20:4	70:10	8∙10	32:4
27:3	21:7	7∙4	8∙3

c∙4=12

6∙c=18

27:c=3

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

70-(7∙3)+(8∙4)

Найди значение выражения, решая по действиям.

64-(27+14)+(6∙4)

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

38+(6∙3)-(4∙7)

Карточка 20

На зиму мама закрыла 4 банки вишнёвого варенья, а малинового — в 3 раза больше. Сколько банок малинового варенья закрыла мама? Сколько всего банок закрыла мама на зиму?

Карточка 21

В первый день маляр покрасил 5 скамеек, а во второй — в 4 раза больше. Сколько скамеек покрасил маляр во второй день? Сколько всего скамеек покрасил маляр за два дня?

Карточка 22

Пятачок за неделю съел 3 баночки мёда, в Винни-Пух — в 3 раза больше. Сколько баночек мёда съел Винни-Пух? Сколько баночек мёда они съели вместе?

Карточка 23

Перед домом посадили 4 ели, а берёз — в 3 раза больше. Сколько посадили берёз? Сколько всего деревьев посадили перед домом?

Карточка 24

Денис нарисовал 16 флажков, а Дима — в 4 раза меньше. Сколько флажков нарисовал Дима? Сколько всего флажков нарисовали мальчики?

Карточка 25

Алёна придумала 12 загадок, а Максим — в 2 раза меньше. Сколько загадок придумал Максим? Сколько всего загадок придумали оба мальчика?

Карточка 26

Мастер за день изготовил 24 детали, а его ученик — в 3 раза меньше. Сколько деталей изготовил ученик? Сколько всего деталей они изготовили вместе?

Карточка 28

На первом острове живёт 32 индейца, а на втором — в 4 раза меньше. Сколько индейцев живёт на втором острове? Сколько всего индейцев на двух островах?

Карточка 29

В куске было 54 метра ткани. Из этой ткани сшили 8 курток, расходуя по 3 метра на каждую. Сколько метров ткани осталось в куске?

В театре ученики первого класса заняли в партере 2 ряда по 9 мест и еще 13 мест в амфитеатре. Сколько всего мест заняли ученики первого класса?

Актовый зал освещает 6 люстр по 8 лампочек в каждой, да еще 7 лам­почек над сценой. Сколько всего лампочек освещает актовый зал?

К празднику купили 4 набора шариков по 10 штук в каждом наборе. Лопнули 12 шариков. Сколько шариков осталось на празднике?

В 3 одинаковых наборах 18 карандашей. Сколько карандашей будет в 7 таких наборах?

Начерти таблицу и реши задачу.

Для изготовления 5 одинаковых конструкторов потребовалось 35 деталей. Сколько деталей нужно для изготовления 8 таких конструкторов?

Начерти таблицу и реши задачу.

Крупу разложили на 6 одинаковых упаковок общей массой 12 кг. Сколько упаковок получится из 20 кг?

Начерти таблицу и реши задачу.

В 3 банки для засолки разложили 12 кг помидоров. Сколько банок потребуется для засолки 32 кг помидоров?

Начерти таблицу и реши задачу.

На 32р. купили 4 тетради. Сколько тетрадей можно купить на 56 рублей? на 16 рублей?

Начерти таблицу и реши задачу.

В 2 ведра помещается 16 кг картофеля. Сколько вёдер нужно, чтобы разложить 24 кг картофеля?

Начерти таблицу и реши задачу.

В 4 наборах 32 листа цветной бумаги. Сколько наборов составляют 72 листа бумаги?

Начерти таблицу и реши задачу.

• Начерти прямоугольник со сторонами 8 см и 4 см. Найди его площадь и периметр.
• Сравни:

12 смc1см2мм	7 мc74 дм	9 ммc1 см
14 смc1дм4см	8см7ммc90 мм	100 смc1 м

• Начерти прямоугольник со сторонами 5 см и 4 см. Найди его площадь и периметр.
• Сравни:

14 смc1см4мм	9 мc94 дм	9 ммc1 см
18 смc1дм8см	6см7ммc70 мм	10 смc1 дм

Расставь знаки «+», «-», «·», «: » так, чтобы равенства стали верными.

26*6*7=13	2*2*4=0
7*9*2=18	8*9*2=70
9*9*2=20	8*4*2=30
9*2*2=16	40*5*7=56

Из 12 м ткани портной сшил 6 одинаковых костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?

Начерти таблицу и реши задачу.

В огороде собрали 24 кг моркови, редиса — в 4 раза меньше, чем моркови, а чеснока — в 5 раз больше, чем редиса. Сколько килограммов чеснока собрали?

Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?

Начерти таблицу и реши задачу.

Итоговая административная контрольная работа

Вариант 1

1. Вычисли

75:5=     203*4=       34:5=

33:3=     900:30=     213:7=

23*4=   760:4=       305:10=

2.Выполни вычисления в столбик

345+276=   818:3=

610-345=     134*4=

3. Реши задачу

В магазине было 115 белых гвоздик и 68 красных. Из них сделали букеты по 3 гвоздики в каждом. Сколько букетов получилось.

4.Задача

Ширина прямоугольника 6 см, а длина на 2 см больше. Найди его периметр и площадь.

5. Сравни, поставь знаки > <, =

1 кг…532г                    5м 2дм… 25 дм

1 сут. … 23 ч                 3дм² …200 см²

6 дм 3 см…630 мм       3 ч … 120 мин

Вариант 2

1. Вычисли

105:7=       305*5=         53:7=

66:6=         100:50=       243:8=

28*4=         960:4=         405:10=

2.Выполни вычисления в столбик

438+178=   714:3=

712-333=   258:3=

3. Реши задачу

С одной грядки собрали 345 кг моркови, а с другой 258 кг. Всю морковь разложили в мешки по 9 кг. Сколько мешков потребовалось?

4.Задача

Длина прямоугольника 7 см, а ширина 2 см меньше. Найди его периметр и площадь.

5. Сравни, поставь знаки > <, =

300г… 1 кг               6м 3дм…66дм

2 сут. …40 ч.             6дм²…600 см²

3дм 2 см…320 см     100 мин … 1 ч