Порядок выполнения действий, правила, примеры

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

• 2 — это первое слагаемое,
• 5 — второе слагаемое,
• 7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

Свойства сложения Переместительное свойство сложения От перестановки мест слагаемых сумма не меняется. a + b = b + a Сочетательное свойство сложения Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа. (a + b) + c = a + (b + c) Свойство нуля при сложении Если к числу прибавить нуль, получится само число. a + 0 = 0 + a = a

На заметку!
При сложении нескольких чисел, их можно объединять в группы и переставлять в любом порядке. Например: a + b + с = (a + b) + c = a + (b + c).

Задачи на умножение-деление в предалах 100.

1. Ученики 1 класса по заданию учительницы взяли в библиотеке по 2 сказки Пушкина. Сколько всего сказок Пушкина выдал библиотекарь второклассникам, если известно, что во втором классе учится 20 человек?

2. Концертный зал имеет 11 рядов, в каждом ряду по 12 кресел. Сколько зрительских мест в этом зале?

3. Чтобы полить одну грядку с огурцами, бабушке нужно 3 л воды. Сколько литров воды потребуется бабушке, чтобы полить 6 таких грядок?

4. В первой банке 12 литров сока. Во второй — в 2 раза меньше. Сколько сока надо перелить из первой банки во вторую, чтобы в обеих банках стало сока поровну? 

5. У белки в дупле заготовлены на зиму  грибы и орехи. Грибов белка заготовила 86 штук, а орехов всего 4 штуки. Во сколько раз больше белка заготовила грибов, чем орехов?

6. Расстояние от глаз телезрителя до экрана телевизора должна быть в 4 раза больше, чем диагональ экрана. каким должно быть это расстояние, если диагональ экрана равна 36 см?

7. Акула за 10 минут проплывает 1 000 м. Какое расстояние она проплывает за 1 минуту?

8. Заяц за час может пробежать 60 км, а волк на 15 км меньше. какое расстояние может пробежать волк за 1 час?

9. Миша каждый день решал по 5 математических задач. Сколько задач Миша решил за неделю?

10. В магазине в понедельник продали 26 сказок Пушкина, а во вторник в 2 раза меньше. Сколько сказок было всего  продано за 2 дня?

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо!!!

Скобка в скобке

Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).

Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение, просто переписывая его как есть. 
Давайте для примера разберем написанное выше задание.

Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).Решение:

\(7x+2(5\)\(-(3x+y)\)\()=\)		Выполнять задание начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относиться – это сама скобка и минус перед ней (выделено зеленым). Всё остальное (не выделенное) переписываем также как было.
\(=7x+2(5\)\(-3x-y\)\()=\)		Теперь раскрываем вторую скобку, внешнюю.
\(=7x+2·5-2·3x-2·y=\)		Упрощаем получившееся выражение…
\(=7x+10-6x-2y=\)		…и приводим подобные.
\(=x+10-2y\)		Готово.

Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).Решение:

\(-(x+3(2x-1\)\(+(x-5)\)\())\)		Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается.
\(-(x+3(2x-1\)\(+x-5\)\())\)		Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке.
\(=-(x\)\(+3(3x-6)\)\()=\)		Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него.
\(=-(x\)\(+9x-18\)\()=\)		Вновь приводим подобные.
\(=-(10x-18)=\)		И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные.
\(=-10x+18\)		Готово.

Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.

Задачи на сложение-вычитание в пределах 20.

1. Поезд прибыл на станцию в 14 часов 19 минут, а должен был согласно расписанию прибыть в 14 часов 14 минут. На сколько минут поезд опоздал?

2. Витя на школьном турнире по шашкам выиграл в 6 партиях, а проиграл в 3. Сколько партий Витя сыграл вничью, если всего он сыграл 12 раз.

3.  Гусь весит 9 кг, а курица на 7 кг меньше. Сколько весят курица и гусь вместе?

4. Бабушка собрала урожай огурцов. Старшей дочери она отвезла 2 ведра огурцов, младшей столько же, а сыну — 3 ведра огурцов. Сколько всего ведер огурцов бабушка отвезла детям?

5. Саша, помогая маме, вымыл 8 тарелок, 4 вилки, 3 кружки и 1 чашку. Сколько всего предметов вымыл Саша?

6. Дима собрал 5 стаканов малины. Бабушка 8 стаканов. На варенье ушло 10 стаканов малины. Сколько стаканов ягоды осталось?

7. В кувшине 4 стакана молока. В бидоне — 8 стаканов молока. За обедом дети выпили 5 стаканов молока. Сколько всего молока осталось? 

8. После обеда Наташа гуляла во дворе 2 часа. Затем она целый час делала домашнее задание. После этого 1 час занималась музыкой и 1 час рисовала. В это время ее позвали ужинать. Во сколько был ужин у Наташи, если обедала она в 2 часа дня.

9. У Ани есть старшая сестра Юля и младший брат Толя. Толе 5 лет. Аня старше его на 3 года. А Юля  старше Толи на 8 лет. На сколько лет Аня младше Юли?

10. На салат пошло 6 огурцов, 5 помидоров и редисок столько, сколько огурцов и помидоров вместе. Сколько всего овощей пошло на салат?

Презентация 2 класса по предмету «Математика» на тему: «Урок математики Тема: «Порядок действий.Скобки» 2 класс Лобова Ольга Викторовна МОУ СОШ с.Васильевка.». Скачать бесплатно и без регистрации. — Транскрипт:

2

Урок математики Тема: «Порядок действий.Скобки» 2 класс Лобова Ольга Викторовна МОУ СОШ с.Васильевка

3

Скобки! Математический знак. Математический знак. Ставятся, упорядочивают, указывают. Ставятся, упорядочивают, указывают. Они сторожа счета. Они сторожа счета. Порядок действий! Порядок действий!

4

Цель: Создать условия для формирования умений применять знания правила порядка выполнения действий в выражениях со скобками в различных ситуациях Создать условия для формирования умений применять знания правила порядка выполнения действий в выражениях со скобками в различных ситуациях

5

Задачи: формировать знания о правилах порядка действий в выражениях со скобками;формировать знания о правилах порядка действий в выражениях со скобками; способствовать развитию умений и навыков решения примеров со скобками; текстовых задачспособствовать развитию умений и навыков решения примеров со скобками; текстовых задач воспитывать у учащихся нравственные качества (организованность и доброжелательность).воспитывать у учащихся нравственные качества (организованность и доброжелательность).

6

Напомните условие задачи по краткой записи: ____________?мин________ ___I_______II_______III___ 10мин. 20мин 10мин 10мин. 20мин 10мин 10+20=30 (мин) 10+30=40 (мин) 10+(10+20)=40 (мин) Ответ: 40 минут тратит папа на дорогу

11

Логика Задача для ума Задача для ума В чудо – мешочке находятся 3 белых и 3 синих шарика. Сколько нужно вынуть шариков из мешочка, чтобы заранее утверждать, что хотя бы 1 будет белым? В чудо – мешочке находятся 3 белых и 3 синих шарика. Сколько нужно вынуть шариков из мешочка, чтобы заранее утверждать, что хотя бы 1 будет белым?

13

малирн +

14

Проблема! 8 – = = 1 1) 2)

15

-Сравните выражения и результаты. Что заметили? — Почему? Как выполняли действия? — Как нам изменить выражения, ведь судя по результату они не равны? Нам необходимо как-то обозначить в записи порядок действий. Предложите свои способы обозначения порядка действий. Может быть надо ограничить, отделить действия одно от другого? 8 –/ 3 + 4/= 1

16

Принято в математике обозначать очерёдность действий с помощью скобок. ( ) Действие которое написано в скобках выполняется первым. 8 — (3 + 4 ) = 1

17

8 – =9 8 – (3 + 4) = 1 1)8-3=5 1)3+4 =7 2)5+4=9 2) 8-7=1

18

Составьте алгоритм действий для решения примеров без скобок и примеров со скобками. Помните, что действие записанное в скобках выполняется первым

19

Алгоритм выполнения действий 1. В скобках 2. По порядку слева направо

23

Задача 7 (стр 23) ____________?____________ ___I_______II_______III___ 39р. ?на 12р. 39р. ?на 12р.

24

Задача 7 (стр 23) ____________?____________ ___I_______II_______III___ 39р. ?на 12р. 39р. ?на 12р. I способ I способ 1)39-12 =27(р.) во втором букете 1)39-12 =27(р.) во втором букете 2)39+4=43(р.) в третьем букете 2)39+4=43(р.) в третьем букете 3) =109(р.) 3) =109(р.)

25

Задача 7 (стр 23) I способ 1)39-12 =27(р.) во втором букете 1)39-12 =27(р.) во втором букете 2)39+4=43(р.) в третьем букете 2)39+4=43(р.) в третьем букете 3) =109(р.) 3) =109(р.) II способ 39+ (39-12)+(39+4)=109(р.) Ответ: 109 ромашек в трех букетах

29

1.Укажите, какое действие будете выполнять первым 8-(3+4) а) + б)- 2. Укажите, какое действие вы будете выполнять последним а) + б) —

30

3. Укажите выражение со значением 40 а) (21+13)-11 б) 75-(20+15) в) (61+20) Расставьте порядок действий в выражениях (78+12) — (12-9) ; а — (в + с)

31

Вспомните тему урока. Что узнали нового? Назовите порядок действий в выражениях без скобок. В выражениях, содержащих скобки. Подведем итог. Чтобы правильно решить выражения со скобками мы должны соблюдать порядок действий. Помнить, что первыми выполняются действия записанные в скобках.

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.

Рассмотрим решения примеров.

Пример.

Выполните действия в выражении (3+1)·2+62:3−7.

Решение.

В этом выражении содержится степень 62, ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 62=36. Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7.

Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7=8+12−7=13.

Ответ:

(3+1)·2+62:3−7=13.

Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.

Список литературы.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6.

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3, получаем 4, после чего к полученной разности 4 прибавляем 6, получаем 10.

Кратко решение можно записать так: 7−3+6=4+6=10.

Ответ:

7−3+6=10.

Пример.

Укажите порядок выполнения действий в выражении 6:2·8:3.

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

сначала 6 делим на 2, это частное умножаем на 8, наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2.

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6, получаем 30, это число делим на 3, получаем 10. Теперь 4 делим на 2, получаем 2. Подставляем в исходное выражение вместо 5·6:3 найденное значение 10, а вместо 4:2 — значение 2, имеем 17−5·6:3−2+4:2=17−10−2+2.

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7.

Ответ:

17−5·6:3−2+4:2=7.

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Какие часто используемые знаки есть на клавиатуре

Если внимательно посмотреть на клавиатуру, то можно увидеть, что многие знаки скрываются в цифровом ряду и с правой стороны буквенных рядов, последние клавиши. Для ввода при печати знаков вместо букв или цифр нужно переключить верхний регистр клавишей Shift.

Если идти по порядку, начиная с цифры 1, то таким способом при печати русских текстов вводится:

1) восклицательный знак «!»;2) открывающиеся и закрывающиеся кавычки в начале и конце фразы «…»;3) затем при необходимости знак номера «№»;4) точка с запятой «;»;5) «%»;6) двоеточие «:»;7) вопросительный знак «?»;8) знак звездочка «*», который используется и как знак умножения при компьютерных вычислениях;9) круглая открывающаяся «(»;10) круглая закрывающаяся скобка «)» на клавише с цифрой 0;11) дефис и знак «-» – в компьютерном варианте выглядят одинаково. Знак тире (более длинный) появляется автоматически с использование пробелов до и после этого знака в текстовых программах или же вводится с помощью специального кода.12) знак равно «=» и знак «+» в верхнем регистре, т.е. в комбинации с клавишей Shift.

Примечательно, что восклицательный знак, %, *, круглые скобки находятся как в русской, так и в английской раскладке клавиатуры на одних и тех же клавишах.

Но некоторые знаки существуют только в английской раскладке. Например, квадратные и фигурные {…} скобки, которые находятся на клавишах с русскими буквами Х (открывающиеся) и Ъ (закрывающиеся), «>» (клавиша с русской буквой Ю) и меньше «Редко используемые знаки на клавиатуре

В повседневной жизни обычному пользователю редко приходится пользоваться знаками, существующими только в английской раскладке: разные варианты кавычек “…”, ‘…’, `…`, черточек «|», прямой «/» и обратный «\» слеш, тильда «~». А вот знак параграфа «§» или градуса «°» не помешал бы , но на клавиатуре их нет. Приходится вводить в текст некоторые символы другим способом.

Большинство пользователей персонального компьютера, которые не очень хорошо владеют программой Word, ставят вместо подлинного знака умножения символ *, а то и вовсе букву х. Конечно же, это абсолютно неправильно. В данной статье дана информация о том, как в «Ворде» поставить знак умножения точкой или крестиком. Именно эти символы являются верными с математической точки зрения.

Правило встречается в следующих упражнениях:

1 класс

Страница 18. Урок 11,
Петерсон, Учебник, часть 1

Страница 10. Урок 6,
Петерсон, Учебник, часть 2

Страница 43. Урок 22,
Петерсон, Учебник, часть 2

Страница 51. Урок 26,
Петерсон, Учебник, часть 2

Страница 9. Урок 5,
Петерсон, Учебник, часть 3

Страница 19. Урок 10,
Петерсон, Учебник, часть 3

Страница 22. Урок 12,
Петерсон, Учебник, часть 3

Страница 35. Урок 18,
Петерсон, Учебник, часть 3

Страница 43. Урок 22,
Петерсон, Учебник, часть 3

Страница 88. Урок 35,
Петерсон, Учебник, часть 3

2 класс

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 24. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 12. Урок 4,
Петерсон, Учебник, часть 2

Страница 24. Урок 8,
Петерсон, Учебник, часть 2

3 класс

Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 97,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 28,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 36,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 50,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 31,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 566,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 567,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1372,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1440,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 242,
Мерзляк, Полонский, Якир, Учебник

Номер 260,
Мерзляк, Полонский, Якир, Учебник

Номер 435,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Номер 949,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 329,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Номер 1099,
Мерзляк, Полонский, Якир, Учебник

Номер 1100,
Мерзляк, Полонский, Якир, Учебник

Номер 1345,
Мерзляк, Полонский, Якир, Учебник

Задание 704,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 705,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1118,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1122,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1511,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·63−2+42.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·63−2+42=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·63−2+42=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Первое правило раскрытия скобок

Рассмотрим выражение:

8 + (−9 + 3)

Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак. Формула раскрытия скобок (a − b) = a — b

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

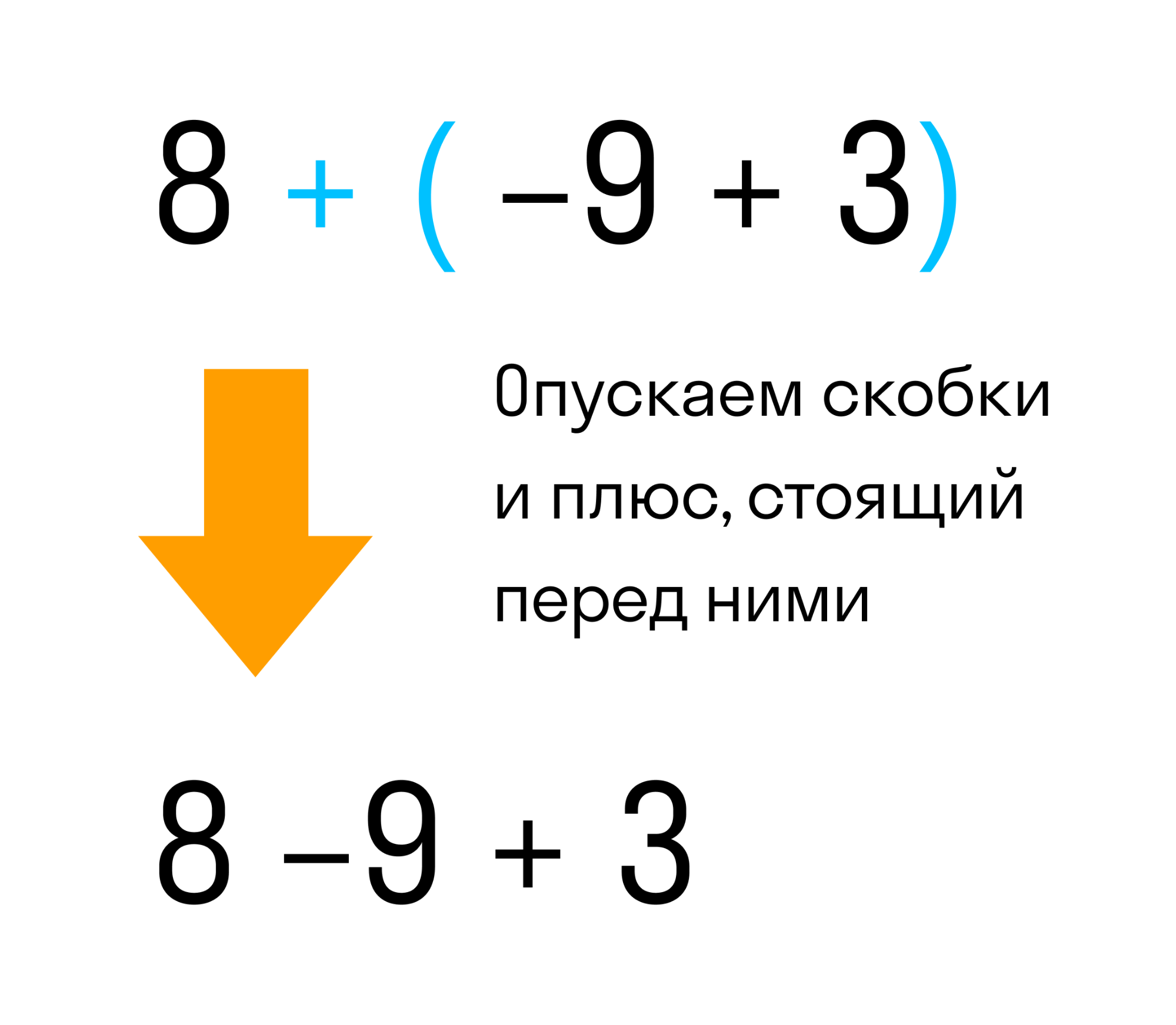
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

• 8 + (−9 + 3) = 2
• 8 − 9 + 3 = 2

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

• 8 + (−9 + 3) = 8 − 9 + 3
• 2 = 2

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Как рассуждаем:

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

8 + (−3 − 1) = 8 − 3 − 1

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Как рассуждаем:

Перед скобками стоит плюс, значит применим то же правило:

6 + (−2) = 6 − 2

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

3a + (−4b) = 3a − 4b

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

2 + (−3 + 1) + 3 + (−6)

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

Как рассуждаем:

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

6 + (−3) + (−2) = 6 − 3 − 2

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении (−7)

Как рассуждаем:

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

(−7) = −7

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Как рассуждаем:

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

9a + (−5b + 6c) + 2a + (−2d) = 5a −5b + 6c + 2a − 2d

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом  или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах

Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3+1)·2+623−7.

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+363−7.

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

(3+1)·2+363−7=4·2+363−7=8+12−7=13

Ответ: (3+1)·2+623−7=13.

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Правила раскрытия скобок

Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря: 

\((a-b)=a-b\)

Здесь нужно пояснить, что в математике для сокращения записей принято не писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не \(+7+3\), а просто \(7+3\), несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.

Пример. Раскройте скобку \((1+y-7x)\).Решение: \((1+y-7x)=1+y-7x\).

Пример. Упростите выражение: \(3+(5-2x)\).Решение: Раскрываем скобку согласно правилу, а затем приводим подобные слагаемые

Пример. Раскройте скобку и приведите подобные слагаемые: \((x-11)+(2+3x)\).Решение: \((x-11)+(2+3x)=x-11+2+3x=4x-9\).

Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:

\(-(a-b)=-a+b\)

Здесь нужно пояснить, что у \(a\), пока оно стояло в скобке, был знак плюс (просто его не писали), и после снятия скобки этот плюс поменялся на минус.

Пример: Упростите выражение \(2x-(-7+x)\).Решение: внутри скобки два слагаемых: \(-7\) и \(x\), а перед скобкой минус. Значит, знаки поменяются – и семерка теперь будет с плюсом, а икс – с минусом. Раскрываем скобку и приводим подобные слагаемые.

Пример. Раскройте скобку: \(-(4m+3)\).Решение: \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).Решение: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть: 

\(c(a-b)=ca-cb\)

Пример. Раскройте скобки \(5(3-x)\).Решение: В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример. Раскройте скобки \(-2(-3x+5)\).Решение: Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).

Пример. Упростить выражение: \(5(x+y)-2(x-y)\).Решение: \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:

\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)