Как разделить участок земли с домом на две части и оформить отдельно?

Деление числа на произведение

Число можно разделить на произведение двумя способами:

1) Чтобы разделить какое-нибудь число на произведение, можно сначала вычислить значение произведения (выполнить умножение), а затем разделить число на полученный результат.

Например, чтобы найти значение выражения:

60 : (3 · 2),

можно сначала умножить  3  на  2:

3 · 2 = 6

и разделить  60  на полученный результат:

60 : 6 = 10,

значит  60 : (3 · 2) = 60 : 6 = 10.

Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение, то можно воспользоваться вторым способом нахождения частного от деления числа на произведение.

2) Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый сомножитель, полученное частное разделить на второй сомножитель, это частное на третий и т. д.

Например, чтобы найти значение выражения:

120 : (5 · 3),

можно сначала разделить  120  на  5:

120 : 5 = 24,

а теперь, полученное частное  24  разделить на  3:

24 : 3 = 8,

значит  120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8.

Так как от перестановки множителей произведение не изменится, то множители можно поменять местами:

120 : (3 · 5)

и разделить  120  сначала на  3,  а затем полученный результат разделить на  5:

120 : (3 · 5) = (120 : 3) : 5 = 40 : 5 = 8.

Получается, что не важно на какой множитель сначала делить число, результат будет одинаковым:

120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8

тоже самое, что и

120 : (5 · 3) = (120 : 3) : 5 = 40 : 5 = 8.

Из данного примера можно сделать вывод, что значение частного не изменится от порядка выполнения действий.

Преимущества разделения как метода размножения

Когда говорят, что размножение комнатных растений — не такой уж и сложный процесс, в первую очередь подразумевают их деление. Из всех видов размножения даже с учетом способности черенков многих культур выпускать корни просто в воде, деление — наиболее доступный и легкий.

У деления комнатных растений есть немало преимуществ:

• в результате удается получить новое растение с уже сформированными корнями, побегами и листьями;
• на адаптацию нового растения уходит минимальное время;
• это самый быстрый способ размножения — деленки тронутся в рост раньше, чем укоренится черенок даже у самых «быстрых» конкурентов;
• это наименее травматичный метод;
• разделение не требует особых навыков.

А единственными, да и то условными недостатками размножения комнатных растений делением остаются потеря материнского куста и ограниченное число новых растений.

Разделение как метод размножения используют как для получения потомства, так и для омоложения взрослых растений с наименьшими усилиями и травмами. fyta

А как быть с числами со знаком?

Числа со знаком, обычно, обрабатывают как числа без знака. При этом для отрицательных значений меняется знак (берется модуль числа).
Как сменить знак числа, если немного забыли, можно почитать в упоминавшейся в начале статье о простых типах данных. Частное от деления
знаковых чисел будет положительно, если делимое и делитель имеют одинаковые знаки. Иначе, частное будет отрицательно, то есть,
ему придется еще раз сменить знак после деления (мы же делили числа без знака, то есть, положительные). Остаток всегда
будет иметь знак делимого. И для отрицательного делимого знак остатка тоже придется подкорректировать.

История и философия ноля

На самом деле история с делением на ноль не давала покоя его изобретателям (а ноль изобрели в Индии). Но индийцы — философы привыкшие к абстрактным задачам. Что значит разделить на ничто? Для европейцев того времени такого вопроса вообще не существовало, так как ни о нуле ни об отрицательных числах (которые левее нуля на шкале) они знать не знали.

В Индии отнять от меньшего большее и получить отрицательное число не составляло проблем. Ведь что значит 3-5=-2 в обычной жизни? Это значит, что кто-то остался должен кому-то 2. Отрицательные числа назывались долгами.

Теперь давайте так же просто разберемся с вопросом деления на нуль. В далеком 598 году нашей эры (только вдумайтесь как давно, более 1400 лет назад!) в Индии родился математик Брахмагупта, который тоже задавался вопросом деления на ноль.

Он предположил, что если взять лимон и начать делить его на части, рано или поздно мы придем к тому, что дольки будут очень маленькими. В воображении мы можем дойти до того, что дольки станут равны нулю.

Итак, вопрос, если разделить лимон не на 2, 4 или 10 частей, а на стремящееся к бесконечности количество частей — какого размера получаться дольки? Получится бесконечное число «нулевых долек». Все довольно просто, нарежем лимон очень мелко, получим лужицу с бесконечным количеством частей — лимонный сок.

Достаточно задать самому себе вопрос:

х/ ∞=0 значит и х/0=∞

Что будет если поделить на ноль?

Но если взяться за математику, то получается как-то нелогично:

а*0=0? А если b*0=0? Значит: а*0=b*0

А отсюда: а=b

То есть любое число равно любому числу. Первая неправильность деления на ноль, идем дальше. В математике, деление считается обратным действием умножения. Это значит, что если мы делим 4 на 2, мы должны найти число, которое при умножении на 2 даст 4.

Делим 4 на ноль — нужно найти число, которое при умножении на ноль даст 4. То есть х*0=4? Но х*0=0! Опять незадача. Получается мы спрашиваем: «Сколько нолей нужно взять, чтобы получилось 4?» Бесконечность? Бесконечное количество нолей все равно даст в сумме ноль.

А деление 0 на 0 вообще дает неопределенность, ведь 0*х=0, где х вообще все что угодно. То есть — бесчисленное множество решений. Так что же получится в итоге?

Простое объяснение из жизни

Вот вам задачка из физики и реальной жизни. Допустим, мы хотим вычислит за сколько времени сможем пройти 10 километров. Значит Скорость * время = расстояние (S=Vt). Чтобы узнать время, расстояние делим на скорость (t=S/V). А что будет, если скорость у нас 0? t=10/0. Будет бесконечность!

Стоим на месте, скорость равна нулю, и с такой скоростью мы будем вечно добираться до отметки в 10 км. Значит время будет… t=∞. Вот и получилась у нас бесконечность!

И в этом примере делить на ноль можно, жизненный опыт позволяет. Жаль, что учителя в школе не могут объяснять такие вещи так же просто.

Еще одно объяснение

Давайте определимся, что такое деление? Например, 8/4 – означает вопрос «сколько четверок, может поместится в восьмерке?» Ответ: «две четверки», то есть математически 8/4=2.

А если задать себе вопрос 5/0=? Сколько нолей поместится внутри пятерки? Да сколько угодно. Бесконечное количество. Делим на ноль и получаем… снова бесконечность.

Но если вместо абстрактных цифр взять материальные вещи, например, яблоко. 6/3 — «если разложить 6 яблок по 3 в ящики, то сколько нужно ящиков?» Ответ: «2 ящика». Идем дальше 4/0 — «если разложить 4 яблока по ноль(!) штук в ящики, то сколько…» Получится, что ящики то не нужны, мы ничего никуда не кладем!

Совсем простое объяснение

Совсем просто, «на пальцах»

10/2=5 10/4=2,5 10/8=1,25 ….Чем больше число в знаменателе, тем меньше результат

10/2=5 10/1=10 10/0,5=20 ….Чем меньше число в знаменателе, тем больше результат, а если взять очень маленькое число? Например, 0,0000001 получится 1 00 000 000. И если пойти дальше в своих размышлениях и уменьшить знаменатель до нуля? В итоге получим что настолько огромное, что будет называться «бесконечность».

Другие методы разделения

Отделить нужный компонент из имеющейся смеси можно и другими способами. 

Приведем несколько примеров:

1. Декантация – механическое отделение твердых веществ от жидких. Производится путем сливания жидкости с осадка. Широко применяется работниками ресторанов — сомелье и барменами.

2. Сушка – тепловое удаление жидкости из смесей. После сушки остается только твердый состав. Часто применяется на производстве непосредственно перед упаковкой продукции.

3. Электрофорез – сложное явление, заключающееся в электрокинетическом перемещении дисперсных частиц в жидком или газообразном веществе под воздействием электрического поля. Электрофорез применяется для разделения и изучения состава смеси в молекулярной биологии, химии и биохимии.

Методов разделения смесей намного больше, нежели описано в этой статье. Существуют очень сложные способы, которые предназначены для выделения из состава веществ со схожими свойствами или имеющихся в критически малых количествах в гетерогенных и гомогенных смесях.

Чердаки и подвалы

Часто сложности вызывает раздел домов, которые имеют чердаки и подвалы. Как разделить дом с подвалом? Отвечая на этот вопрос, нужно уяснить, каково назначение подвала. Если это нежилое помещение, то подвал может быть разделен, исходя из границ образовавшихся частей дома. А вот говоря о том, как разделить дом с жилым подвалом, нужно включать его площадь в «общий зачет», то есть учитывать его, как жилое помещение. Аналогичная ситуация и с чердаками.

На практике часто бывает так, что разделить на две квартиры в строгом соответствии с идеальными долями не представляется возможным. Какое-то отхождение от этих долей, все равно, присутствует. В этом случае, тот, кто получил долю больше, чем ему причитается, имеет право на получение денежной компенсации. О желании получить компенсацию это лицо должно сообщить в исковом заявлении или в соглашении о разделе недвижимости. Разделив дом, сторонам нужно решать вопрос и о разделе земельного участка. Так как, строение и земля связаны друг с другом. Но это, как говорят, совсем другая история.

Проверка результата деления чисел делением

Рассмотренный выше способ проверки основан на умножении. Существует также проверка делением. Как ее проводить?

Проверка результата деления

Чтобы проверить верно ли найдено частное, нужно делимое разделить на полученное частное. В результате должен получится делитель.

Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.

Правило основано на той же связи между делимым, делителем и частным, что и правило из предыдущего пункта.

Рассмотрим примеры.

Пример 17. Проверка результата деления натуральных чисел

Верно ли равенство:

104÷13=8.

Разделим делимое на частное:

104÷8=80+24÷8=80÷8+24÷8=10+3=13.

В результате получился делитель, значит, деление выполнено верно.

Пример 18. Проверка результата деления натуральных чисел

Вычислим и проверим: 240÷15=?

Представляя делимое в виде суммы, получаем:

240÷15=150+90÷15=150÷15+90÷15=10+6=16.

Проверяем результат:

240÷16=?

240÷16=160+80÷16=160÷16+80÷16=10+5=15.

Деление выполнено верно.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Как разделить дом в натуре

Начиная процесс раздела необходимо заказать строительно-техническую экспертизу, чтобы определить можно ли выделить каждому собственнику отдельную площадь с отдельным входом.

Все изменения должны быть отражены в заключении эксперта:

1. можно ли выполнить техническую часть раздела;
2. варианты возможных перепланировок;
3. стоимость строительных работ;
4. размер компенсации в случае невозможности поделить объект в соразмерном соотношении частей;
5. оценка рыночной стоимости делимого в натуре объекта.

После заключения экспертизы необходимо получить разрешение на ввод реконструированного объекта в эксплуатацию и технический план здания. Если возможно разделить дом, а прилегающий земельный участок стоит на кадастровом учете, то можно разделить и земельный участок. Выделенные участки не должны менять вид разрешенного пользования.

Кадастровый инженер определяет границы и размер каждого участка. Если размер выделенного участка небольшой необходимо обратиться в муниципалитет, с целью узнать минимум, который установлен в регионе относительно размера наделов (Федеральный закон от 24.07.2002 № 101-ФЗ)

На сколько долей можно разделить дом

При разделе дома на доли необходимо учитывать условия осуществления раздела, установленные нормами ст. 252 ГК РФ и заключения строительно-технической экспертизы. Раздел возможен, если:

• отсутствует запрет на деление недвижимости;
• не ухудшатся общие технические характеристики объекта;
• не изменится целевое назначение выделенных частей;
• цена отдельных долей равна рыночной стоимости цельного объекта;
• отдельно выделенные помещения оборудованы индивидуальным входом и удобны для проживания.

Законом предусмотрено, что совместная собственность делится максимум на три части. При четырех и большем количестве совладельцев используются другие способы распределения имущества.

Минимальная норма жилой площади при разделе

В соответствии со статьей 38 Жилищного кодекса РФ норма жилой площади равна 12 квадратных метров при расчете на одного человека. Данный показатель имеет различные значения в зависимости от целей его применения и региона.

Если площадь помещения выделенной доли менее установленной нормы раздел допускается

Важное условие, чтобы были соблюдены все технические и санитарные нормы

Разделы: какие и сколько нужны?

Собственно, никаких ограничений здесь нет. Разве что с точки зрения здравого смысла. Многое зависит от объема вашего диска. Например, террабайтник не стоит делить больше, чем на 2 раздела. Диски от 2 Тбайт можно «порезать» и на 3

Важно лишь понять, для чего они будут служить. Вот один из возможных вариантов деления. 

• Системный (от 500 Гбайт) — для работы системы и софта;
• Основной — для хранения файлов, документов;
• Медиа — для хранения фильмов, фотографий, видео;
• Игры — тут без комментариев. 

Слишком много разделов тоже плохо — скорее всего, они будут маленькими и быстро начнут переполняться. 

Способы деления

Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.

1. С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:

   4 + 4 + 4 = 12,

   следовательно, 4 содержится в 12 три раза.

2. С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:

   12 — 4 = 8
   8 — 4 = 4
   4 — 4 = 0

   Отсюда находим, что можно вычесть 4 из 12 ровно три раза.

   Деление есть сокращенное вычитание равных вычитаемых.

3. Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.

Деление нуля на целое число

Деление нуля на любое целое число рассматривается как отдельная тема, так как имеет свои нюансы. По правилу частное от деления на любое целое число, отличное от нуля, равно нулю. Иначе можем записать, что b=, где значение числа b отлично от нуля.

Для углубления в правило рассмотрим некоторые пояснения.

Допустим, что результат деления нуля на целое число равен с, тогда равенство b·c= считается верным. Произведение в итоге дает ноль тогда, когда хотя бы один из них равен нулю. Если по условию b не равно нулю, тогда множитель с=. Отсюда следует, что  частное, полученное делением нуля на целое число, отличное от нуля, равняется нулю.

Например, при делении нуля на целое число, частное получаем равное нулю: 4 или -908. Оба результаты будут равны нулю.

Как разделить по диагонали при помощи формата.

Разберем пошагово, как разбить по диагонали ячейку при помощи форматирования:

1. Вызываем меню «Формат ячеек». На вкладке «Шрифт» определяем применяемый шрифт и его размер.
2. На вкладке «Граница» выбираем тип линии.
3. Здесь же кликаем на диагональную линию в окне «Отдельные».

1. При необходимости можно красиво расположить текст, чтобы он был как бы разделён наклонной линией. Это часто используют для шапки таблицы в первой колонке.

На вкладке «Выравнивание» в окне «Ориентация» вы можете изменить наклон текста, чтобы получилось нечто подобное тому, что вы видите на скриншоте выше.

1. Подтверждаем действие нажатием «ОК».

Замечание: при таком способе разбиения Excel по-прежнему воспринимает объект как одну клетку.

Правила деления целых чисел

Смысл деления необходим для утверждения того, что одним из двух множителей является частным, а другой просто множителем. Таким образом не найти неизвестный множитель, имея известный множитель  и произведение. Равенство 6·(−7)=−42 говорит о том, что результаты  (−42)6 и (−42)(−7) равняются -7 и 6 соответственно. При известном произведении 45, а одного из множителей -5, то смысл деления не даст прямого результата другого множителя.

Можно сделать вывод, что необходимо использовать правила, которые позволяют производить деление целых чисел. Они позволят делить целые и натуральные числа.

Как разделить десятичную дробь на натуральное число столбиком

Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.

Определение 1

Для деления столбиком десятичных дробей на натуральные числа необходимо:

1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).

2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.

Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.

Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.

Пример 5

Вычислите, сколько будет 65,144.

Решение

Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65,1400, которая будет равна исходной. Теперь пишем столбик для деления на 4:

Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:

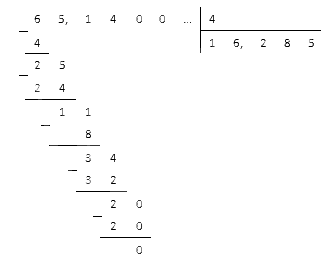
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.

Ответ: 65,144=16,285.  

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 6

Разделите 164,5 на 27.

Решение 

Делим сначала дробную часть и получаем:

Отделяем полученную цифру запятой и продолжаем делить:

Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби 6,(925).

Ответ: 164,527=6,(925).

Как разделить дом на доли

Итак, супружеские отношения испортились, и муж с женой планируют разделить имущество. Что им нужно для этого сделать.

• Варианты таковы:
• Пойти к нотариусу и заключить соглашение о разделе имущества. Это, можно сказать, вариант очень «цивилизованный». Так поступают пары, которые не хотят ссор и скандалов, которые расстаются по-доброму. Для заключения соглашения, нужно явиться к нотариусу с паспортами, документами на дом, свидетельством о браке или его расторжении.
• Обратиться с иском в суд. Исковое заявление подается в суд по месту расположения имущества. Оплачивается госпошлина, которая рассчитывается, исходя из стоимости спорного имущества. Решение суда вступает в силу, спустя 1 месяц со дня его вынесения.

На основании соглашения или решения суда осуществляется регистрация права собственности в органах Росреестра, выдаются соответствующие свидетельства об этом. Встречается и другая ситуация, когда дом делится на доли. Например, собственник желает подарить часть своего недвижимого имущества некоему лицу. В таком случае, у прежнего собственника остается доля дома, а у нового собственника доля дома появляется. Такие «манипуляции» тоже требуют обращения в органы Росреестра, чтобы прошла регистрация права собственности на доли дома.

Юридическая помощь по разделу недвижимости

Консультация в офисе и по телефону

Помощь адвоката. Стаж 18 лет по разделу недвижимости!

Работаем в период карантина 2021 года! Звоните.

Как можно доказать признак делимости на 2

Перед тем, как перейти непосредственно к доказательству этого признака, нам надо доказать дополнительное утверждение. Оно формулируется так:

Определение 2

Все натуральные числа, которые заканчиваются на нуль, могут быть разделены на два без остатка.

Пользуясь правилом умножения натурального числа на 10, мы можем представить некое число a как a=a1·10. Число a1, в свою очередь, получится из a, если убрать у него последнюю цифру.

Приведем примеры такого действия: 470=47·10, где a=470 и a1 =47; или же 38 010·10, здесь a=380 100 и a1=38 010. Второй множитель в этом произведении (10) может быть разделен на 2, значит, все произведение может быть разделено на 2. Это утверждение основано на соответствующем свойстве делимости.

Переходим к доказательству признака делимости на 2. Чтобы было удобнее, представим его как теорему, т.е. как необходимое и достаточное условие делимости целого числа на два.

Теорема 1

Для деления целого числа a на два необходимым и достаточным условием является наличие последней цифры , 2, 4, 6 или 8.

Доказательство 1

Как доказать это утверждение? Для начала представим исходное число a в виде суммы десятков и единиц, т.е. запишем его как a=a1·10+a. Здесь a1 будет числом, получившимся из a при устранении последней цифры, а a соответствует последней цифре данного числа (примерами такого представления также могут быть выражения 49=4·10+9, 28 378=2 837·10+8). Произведение a1·10, взятое из равенства a=a1·10+a, всегда будет делиться на два, что и показано с помощью этой теоремы.

Остальная часть доказательства основана на определенном свойстве делимости, а именно: если у нас есть три числа, образующие равенство t=u+v, и два из них делятся на целое число z, то и третье число также можно разделить на z.

Если a можно разделить на два, то согласно этому свойству, а также представлению a=a1·10+a, число a будет делиться на два, а такое возможно, только если a= , 2, 4, 6 или 8.

А если a на 2 не делится, то исходя из того же самого свойства, число a на 2 тоже делиться не будет, что возможно только при a = 1, 3, 5, 7 или 9. Это и есть нужное нам доказательство необходимости.

Теперь разберем обратную ситуацию. Если у нас есть число a, последней цифрой которого является число , 2, 4, 6 или 8, то a делится на 2. Указанное свойство делимости и представление a=a1·10+a позволяют нам заключить, что a делится на 2. Если a имеет последнюю цифру 1, 3, 5, 7 или 9, то то a не делится на 2, значит, a тоже не делится на 2, иначе само представление a=a1·10+a делилось бы на 2, что невозможно. Достаточность условия доказана.

В конце отметим, что числа с последней цифрой 1, 3, 5, 7 или 9 при делении на два всегда дают в остатке единицу.

Возьмем случай, когда заданное число кончается одной из этих цифр. Тогда мы можем представить a как a=b+1, при этом число b будет иметь в качестве последней цифры , 2, 4, 6 или 8. В силу признака делимости на 2 число b можно разделить на 2, значит, по определению делимости оно также может быть представлено в виде b=2·q, где q будет некоторым целым числом. Мы получили, что a=2·q+1. Данное представление показывает нам, что при делении числа a на 2 получается неполное частное q и остаток 1 (если нужно, перечитайте статью о делении целых чисел с остатком).

Правило деления целых отрицательных чисел, примеры

Для формулировки правила необходимо применить рассуждения. Если необходимо поделить целые отрицательные числа a на b, то искомое частное получится равным с. Форма записи: ab=c. После чего можно выяснить, чему равна абсолютная величина с.

Исходя из смысла деления равенство b·c=a справедливо. Значит, b·c=a. Благодаря свойствам модуля, можно записать равенство b·c=b·c, значит, и b·c=a. Отсюда получаем, что c=ab. Абсолютная величина частного от деления равняется частному от деления модулей делимого и делителя.

Для определения знака числа с необходимо выяснить, какие знаки находятся перед делимым и делителем.

Исходя из смысла деления целых чисел, равенство b·c=a справедливо. Правило умножения целых чисел говорит о том, что частное должно быть положительным. Иначе, b·c будет производиться по правилам целых отрицательных чисел. Частное с от деления целых отрицательных целых чисел является положительным числом.

Объединить в правило деления: чтобы разделить целое отрицательное число на отрицательное, необходимо разделить делимый на делитель по модулю. Эта запись будет выглядеть так ab=ab, при а и b равными отрицательным числам.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Рассмотрим несколько примеров деления отрицательных чисел.

Пример 3

Разделить -92 на -4.

Решение

Используя правила деления целых отрицательных чисел, получим, что следует делить по модулю. Получим, что -92-4=-92-4=924=23

Ответ: (−92)(−4)=23.

Пример 4

Вычислить -512 (-32).

Решение

Для решения необходимо разделить числа по модулю. Деление производится столбиком.

Ответ: (−512)(−32)=16.

Деление на 10, 100, 1000 и т. д.

Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого. Этого мы достигаем, отделяя запятою цифру единиц. Число до запятой будет выражать частное, а после запятой — остаток.

Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:

Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.

Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.

Как увеличить системный раздел, не форматируя диск

Еще один типичный случай: на вашем компьютере уже есть диск с несколькими разделами, в которых размещена информация. Однако Windows и программы настолько разрослись, что свободного места в системном разделе совсем не осталось. Не торопитесь бежать в магазин за новым винчестером — выход есть. Соседние разделы можно слегка ужать за счет незанятого пространства и передать высвобожденное место под файловую систему.

Однако перед подобной операцией настоятельно рекомендуем выполнить его очистку от ненужных файлов — например, утилитой CCleaner. Затем остается только приступить к перераспределению пространства. В Windows 7 и Windows 10 это можно сделать штатными средствами.

1. Одновременно нажмите клавиши «Win» и «R», чтобы открыть командную строку.
2. Введите в строке «compmgmt.msc» и нажмите «OK». Откроется вкладка «Управление компьютером».
3. Слева зайдите в пункт «Управление дисками», чтобы просмотреть все доступные диски и их разделы.
4. Кликните правой кнопкой мыши на жесткий диск, раздел которого требуется сжать, и выберите «Сжать том».
5. Теперь укажите, насколько вы хотите сжать раздел. Логично, что размер раздела можно уменьшить только на значение, которое не больше объема свободного пространства на диске. Это означает, что если у вас жесткий диск объемом 300 Гбайт, а из них занято 200 Гбайт, вы сможете сжать раздел на 100 Гбайт. Windows автоматически задаст максимальное значение в мегабайтах.
6. Подтвердите действие, нажав кнопку «OK». После этого раздел будет сжат.

После сжатия раздела нераспределенное пространство обозначается как «Не распределен». Именно оно и станет новым разделом.

• Щелкните правой кнопкой мыши на поле «Не распределен» и выберите «Создать простой том».
• Следуйте инструкциям «Мастера создания простого тома» и укажите размер нового раздела и файловую систему, которую вы хотите использовать.
• После этого новый раздел будет создан и доступен под новой (назначенной вами) буквой диска.

Чтобы разбить диск на разделы, также можно использовать программу MiniTool Partition Wizard.

Удобно, что помимо самой программы производитель предлагает на своем интернет-ресурсе абсолютно бесплатно еще и образ загрузочного диска. При установке не забудьте выбрать пункт «Настройка параметров» и отключить установку Яндекс браузера и расширений к нему.

Интерфейс утилиты довольно простой и даже базовых знаний английского достаточно, чтобы выполнить необходимые операции. В качестве альтернативы можно воспользоваться еще одним приложением, позаимствованным из мира Linux, — Gparted. Локализованный интерфейс можно получить в настройке ОС при старте загрузочного диска.

1. После запуска программы выберите диск, расположенный справа от системного раздела, и в контекстном меню нажмите на «Move/Resize».
2. В появившемся окне потяните мышью за левый край полосы дискового пространства и сдвиньте его вправо — до размера, необходимого для расширения системного диска. Скорректировать получаемый объем можно в поле «Unallocate Space Before». Нажмите «ОK».
3. Затем выберите системный диск С: и в контекстном меню опять нажмите на «Move/Resize». Потяните правый край полосы дискового пространства до конца вправо. Нажмите «ОK».
4. Итак, все готово: чтобы расширить ваш системный раздел С:. Кликните в верхнем меню по значку «Apply». Если информации в разделах было накоплено много, то процесс может быть длительным — позаботьтесь о том, чтобы питание компьютера не было отключено.

• Как правильно покупать ноутбук «с рук»?
• Проверь работу компьютера: лучшие бесплатные утилиты для теста ПК
• 4 полезные программы для работы с жесткими дисками

Как распределить текст с разделителями на множество столбцов.

Изучив представленные выше примеры, у многих из вас, думаю, возник вопрос: «А что, если у меня не 3 слова, а больше? Если нужно разбить текст в ячейке на 5 столбцов?»

Если действовать методами, описанными выше, то формулы будут просто мега-сложными. Вероятность ошибки при их использовании очень велика. Поэтому мы применим другой метод.

Имеем список наименований одежды с различными признаками, перечисленными через дефис. Как видите, таких признаков у нас может быть от 2 до 6. Делим текст в наших ячейках на 6 столбцов так, чтобы лишние столбцы в отдельных строках просто остались пустыми.

Для первого слова (наименования одежды) используем:

Как видите, это ничем не отличается от того, что мы рассматривали ранее. Ищем позицию первого дефиса и отделяем нужное количество символов.

Для второго столбца и далее понадобится более сложное выражение:

Замысел здесь состоит в том, что при помощи функции ПОДСТАВИТЬ мы удаляем из исходного содержимого наименование, которое уже ранее извлекли (то есть, «Юбка»). Вместо него подставляем пустое значение «» и в результате имеем «Синий-M-39-42-50». В нём мы снова ищем позицию первого дефиса, как это делали ранее. И при помощи ЛЕВСИМВ вновь выделяем первое слово (то есть, «Синий»).

А далее можно просто «протянуть» формулу из C2 по строке, то есть скопировать ее в остальные ячейки. В результате в D2 получим

Обратите внимание, жирным шрифтом выделены произошедшие при копировании изменения. То есть, теперь из исходного текста мы удаляем все, что было уже ранее найдено и извлечено – содержимое B2 и C2

И вновь в получившейся фразе берём первое слово — до дефиса.

Если же брать больше нечего, то функция ЕСЛИОШИБКА обработает это событие и вставит в виде результата пустое значение «».

Скопируйте формулы по строкам и столбцам, на сколько это необходимо. Результат вы видите на скриншоте.

Таким способом можно разделить текст в ячейке на сколько угодно столбцов. Главное, чтобы использовались одинаковые разделители.

Заключение

Деление считается самой сложной операцией из четырех арифметических. И в виде готовой команды микроконтроллера оно встречается реже всего.
Но программная реализация оказалась вовсе не такой страшной, хотя и очень медленной по сравнению с аппаратно реализованными командами.
Для деления на известные на этапе написания программы константы лучше использовать комбинации сдвигов/вычитаний/сложений.
Увеличение
разрядности делимого не вызывает особых проблем и не ведет к резкому увеличению размера программ. Увеличение разрядности делителя гораздо
серьезнее, но непреодолимых трудностей тоже нет. Если же требуется делить числа с разрядностью многократно превышающей разрядность
микроконтроллера, то действительно имеет смысл задуматься о его замене на более подходящий.

Отмечу преимущество нашей реализации деления перед операцией деления в языках высокого уровня — мы сразу получаем и частное, и остаток. Да,
в stdlib есть функция div, которая тоже позволяет получить и частное, и остаток (структура div_t). Но, во первых, не
во всех компиляторах эта библиотека доступна. Во вторых, посмотрите на такую шедевральную, иначе и не скажешь реализацию
функции div в одном из компиляторов для 8-разрядных микроконтроллеров PIC

    div_t div(signed int numer, signed int denom) {
        div_t val;
        val.quot = numer / denom;
        val.rem = numer - (denom * val.quot);
        return (val);
    }

В 8 разрядных PIC команды деления нет, значит оно выполняется только программно. Как мы видели, при этом получается и частное,
и остаток. Но в этой реализации остаток предпочитают получать еще раз, причем через умножение! Замечу, что команда умножения есть
не во всех 8 разрядных PIC. Я не буду называть компилятор и его производителя. Но замечу, что это коммерческий компилятор, и
совсем не дешевый. Поэтому, знать описанные в этой статье алгоритмы деления может быть полезно даже в том случае, если Вы используете другие
контроллеры и всегда пишете программы только на языках высокого уровня.

Вы можете обсудить данную статью или задать вопросы автору на форуме