Деление столбиком

Правила вычитания в столбик

Чтобы найти разность двух и более чисел с любым количеством разрядов можно выполнить вычитание в столбик. Для этого:

1. Записываем уменьшаемое в самой верхней строчке.
2. Под ним записываем первое вычитаемое – таким образом, чтобы одинаковые разряды обоих чисел находились друг под другом (десятки под десятками, сотни под сотнями и т.д.)
3. Таким же способом дописываем другие вычитаемые, если они есть. В результате образуются столбцы с разными разрядами.
4. Под записанными числами чертим горизонтальную линию, которая будет отделять уменьшаемое и вычитаемые от разности.
5. Переходим к вычитанию цифр. Эта процедура выполняется справа налево, отдельно для каждого столбца, а результат пишем под чертой в том же самом столбце. Здесь есть пара нюансов:
   • Если из цифры в уменьшаемом нельзя отнять цифры в вычитаемых, значит занимаем десяток у более старшего разряда, и затем обязательно учитываем это в дальнейших действиях (см. Пример 2).
   • Если в уменьшаемом стоит ноль, это автоматически означает, что для выполнения вычитания нужно занять у следующего разряда (см. Пример 3).
   • Иногда в результате “займа” в более старшем разряде может не остаться цифр (см. Пример 4).
   • В редких случаях, когда вычитаемых много, требуется занять не один, а сразу два и более десятка (см. Пример 5).

Буквенные выражения

 Три весёлых поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф приглашают нас с вами, ребята, в гости. Посмотрите, какие дома они построили!

Как вы думаете, можно ли вставить в окошки карточки с цифрами? Почему?

В домике Ниф-Нифа в открытом окошке может быть карточка с цифрой 5? Какое выражение можно записать?

5 + 4

А какое выражение запишем, если в доме Нуф-Нуфа в окошке будет цифра 2?

6 + 2

Можно ли в окошке Наф-Нафа увидеть цифру 1? А цифру 3?

С цифрой 1 запишем выражение: 1 – 1.

А вот цифра 3 не подходит, потому что из 1 нельзя вычесть 3.

Запишите получившиеся выражения и найдите их значения.

5 + 4= 9

6 + 2= 8

1 – 1= 0

Мы записали числовые выражения, ведь они содержат только числа.

Ребята, как вы думаете, можно ли в окошко вставить карточку с буквой?

В математике принято использовать латинские буквы. Может быть, вы уже знаете некоторые из них? Давайте, правильно назовем латинские буквы.

В окошки домиков поросят подставим карточки с буквами: x, y, d.

Запишем выражения: x + 4, 6 + y, 1 – d.

У нас получились буквенные выражения.

Найдём значение следующих буквенных выражений: 8 + а, d – 6, x + 5, y – 1.

Для этого вместо буквы подставим число: а = 12, d = 9, x = 14, y = 20.

8 + a d – 6 x + 5 y – 1

8 + 12 = 20 9 – 6 = 3 14 + 5 = 19 20 – 1 = 19

Найдите значение выражения: k + 20, если k = 3, k = 5, k = 9.

3 + 20 = 23

5 + 20 = 25

9 + 20 = 29

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

Еще один пример деления

Как записывать деление в столбик

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как объяснить ребенку, что такое умножение и деление

Причина непонимания умножения и деления в большинстве случаев кроется в банальном отсутствии внимательности у школьника

В раннем возрасте деткам сложно концентрировать внимание на чем-то конкретном более 15 минут, поэтому они поддаются влиянию различных отвлекающих факторов

Обратите внимание! Ребенок может стесняться задавать учителю один и тот же вопрос несколько раз, потому что боится показаться глупым в глазах окружающих. В такой ситуации нужно провести со школьником беседу, уточнить детали, которые ему непонятны после объяснения материала, и успокоить

Для того чтобы объяснить ребенку понятие «умножение», для начала нужно подготовить распечатку таблицы умножения Пифагора (нарисовать ее собственноручно или распечатать на принтере). Без такой таблицы не получится разъяснить сам принцип только с помощью обычных примеров. На начальном этапе пусть ребенок сам постарается определить закономерность (желательно, чтобы это занятие стало увлекательной игрой).

Изучая данный раздел математики, детишкам должны быть известны такие простые действия, как сложение и вычитание. Разъясняя своему чаду принцип работы умножения, рекомендуется использовать самый элементарный прием. Нужно разобраться, что фраза «умножить число шесть на число два» или же «шестью два» означает то же самое, что и «шесть плюс шесть». Также следует записать пример в виде цифр для визуализации: 6*2 = 6+6.

Таблица умножения Пифагора

Объяснение принципа деления

Для того чтобы разъяснить ребенку, как нужно правильно делить, совсем необязательно использовать скучные учебники. Вместо них можно взять яблоки, конфеты и игрушки. Взрослый должен попросить карапуза разделить между тремя – четырьмя куклами пять конфеток или яблок, а далее количество фруктов следует постепенно увеличивать до 8-10.

Важно! Малыш сначала будет раскладывать предметы медленно, делая большие паузы, но кричать на него категорически запрещено, лучше запастись терпением. После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог

Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну»

После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог. Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну».

Еще один игровой пример представлен делением на цифрах. Нужно сказать карапузу, что цифры – это те же фрукты или конфеты и приучать, что количество сладостей, которые следует разделить, принято называть «делимое». А люди, на которых делятся конфеты, – это «делитель».

Алгоритм деления столбиком на двузначное число

1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака. 

           Примеры        768:24. Первое неполное делимое 76                                265:53  26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.

2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.

           Примеры       768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.                                265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.                               15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.

3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.

Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.

4. Находим остаток (если есть).

Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.

Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)

Как объяснить ребенку деление и научить делить столбиком?

дети-школьники тренируются делить числа столбиком

Во-первых, учтите ряд вводных факторов:

• ребёнок знает таблицу умножения
• хорошо разбирается и умеет применять на практике действия вычитания и сложения
• понимает разницу между целым и его составными элементами

Дальше акценты в ваших действиях выглядят так:

• поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
• объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
• превратите процесс в игру, придумайте историю про цифры и действие деления,
• подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
• первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:

• запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
• предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
• подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
• помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
• следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
• снова помогите с записью действия,
• продолжайте до момента, когда результат от разницы составит ноль. Это актуально только для деления чисел без остатка,
• закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.

Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.

Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:

• Сначала запишите задачу обычным способом: 250:2=?
• Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
• Затем сделайте сокращенную запись столбиком (уголком):

• Рассуждайте вместе так: сначала найдем неполное частное. Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
• После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.

Желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике. Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.

Итак, как объяснить ребенку деление столбиком:

• Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
• Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
• Пусть ребенок сам разделит другое число, например, более сложное: 24:4
• Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Основные понятия

Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.

Название числа напрямую зависит от количества знаков.

• Однозначное — состоит из одного знака
• Двузначное — из двух
• Трехзначное — из трех и так далее.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.

Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.

В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения 1. От перестановки множителей местами произведение не меняется. a * b = b * a 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c) Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.

Важно помнить правило: умножение в столбик с нулями дает в результате ноль

а * 0 = 0, где а — любое натуральное число.

Алгоритм умножения в столбик

Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:

1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.

2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения

Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д

3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.

Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.

5. Складываем то, что нашли и получаем ответ.

Умножение на однозначное число

Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше. 

Возьмем пример 234 * 2:

1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.

2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.

3. Ответ запишем под чертой:

Производить действия необходимо в следующей последовательности:

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041. 

Примеры на умножение в столбик

Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость

Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем

Повтори тему — деление в столбик, она очень полезная!

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Онлайнумножить столбиком

Для понимания процесса умножения в столбик, мы написали специально для вас скрипт, который умеет умножать в столбик!

умножать в столбик онлайнлибо вы можете сразу перейти

Разберем пример умножения 123 на 456.

После нажатия на кнопку умножить в столбик онлайн вы получаете такую картинку:

№1

До первой горизонтальной линии справа, вы увидите два числа, которые вы собираетесь умножить в столбик онлайн.

слева, знак умножения “X”.

№2

Между первой и второй горизонтальной линиями мы видим два слова, где умножаем, где складываем.

№3

Смотрим на второе число, в пункте №1 – 456, берем последнее число, либо первое справа – как вам нравится. Это 6.

Умножаем его на 123.

Будет присвоен отдельный цвет.

123 Х 6 = 738 – будет записано слева.

И справа будет продублирован результат с отступом справа, чтобы крайнее число результата находилось под тем числом, на которое умножаем.

Далее берем вторую цифру справа 456 – это будет 5… повторяем все действия, что были проделаны с первым числом.

До тех пор, пока число не кончится…

Все числа справа складываем в столбик.

№4

Получаем результат.

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

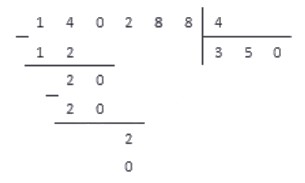
3. Выполняем операцию вычитания  и под чертой записываем результат.

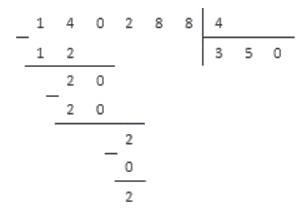
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

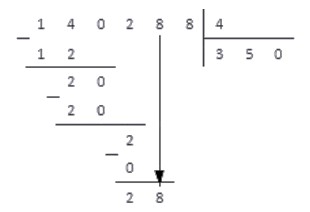
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

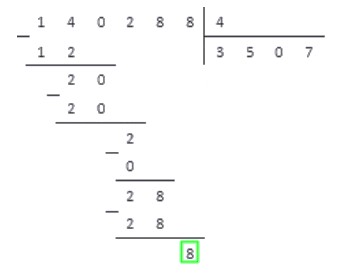
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

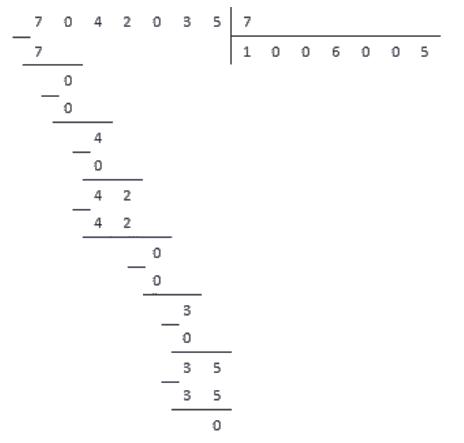
Ответ: 1006005