Деление в столбик

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Принципы деления для детей в доступной форме

Убедившись в том, что азы усвоены надежно, необходимо перейти к доведению до сознания ребенка понимания сути деления. У ребенка должно сформироваться четкое понимание того, что деление – это процесс раздела чего угодно на равные части. Самым простым примером станет выполнение ребенком просьбы взрослого поделить между близкими ограниченное количество каких-либо предметов, к примеру, конфет или мандарина на дольки, так, чтобы всем досталось поровну. Игровая форма при этом процессе весьма желательна и приветствуется. Сначала ребенок станет выдавать по одной штучке (дольке), затем ему предлагается сосчитать общее количество предметов, которое присутствовало изначально, до раздела и какое количество досталось каждому после. Необходимо объяснить на этом наглядном примере, что умение делить заключается в том, чтобы всем досталось поровну, вне зависимости от количества участвующих. Здесь же стоит пояснить, что такое остаток, который может возникнуть при делении. Например, раздел 7 конфет между 3 друзьями приведет к тому, что у каждого будет по 2, а в остатке 1.

512	8	=
делимое	делитель	частное

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

на доске решены примеры на деление столбиком трёх- и более значных чисел

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

алгоритм деления столбиком четырёхзначного числа

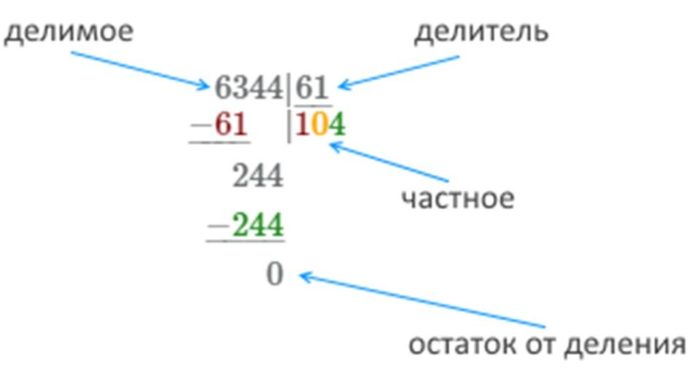
пример деления столбиком четырёхзначного числа на двузначное

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

Примеры подробного решения ниже.

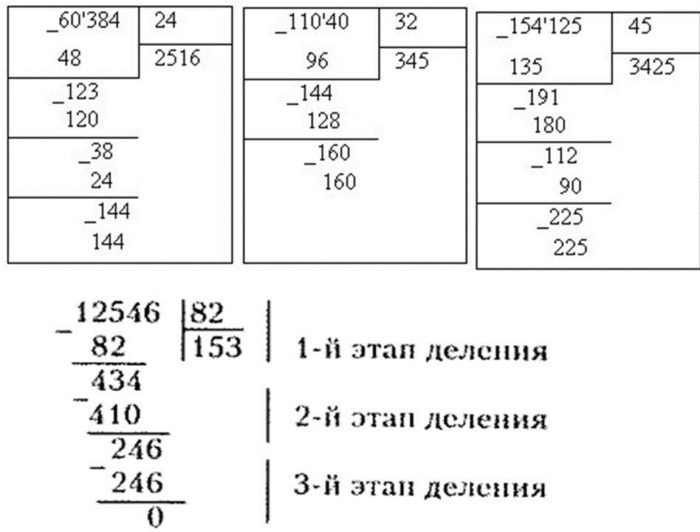
примеры деления столбиком многочленов

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

примеры деления многочленов в столбик

Обучение делению чисел столбиком с нолями

Деление чисел с нолями идентично обычному делению. Родителям нужно объяснить ребенку основные нюансы:

• Расскажите, что если в конце делимого и делителя есть ноли, то их можно зачеркивать в уме. Предложите школьнику зачеркивать их простым карандашом для понимания. Дальше нужно делить, как и в обычных примерах. Например, если 1200 нужно разделить на 400, то ребенок может сократить пример, убрав два 0 у обоих чисел. А в примере деления 15600 на 560 можно сократить только по одному 0.
• Объясните ученику, что если 0 есть только в делителе, то его нельзя сокращать.

Чтобы лучше усваивать материал, можно решить простой пример деления:

• Запишите в тетради пример: 100 разделить на 10. Это легкий пример, так как при сокращении нолей он представлен так: 10 разделить на 1.
• Ребенку следует под делителем написать цифру 10. Так как при умножении 1 на 10 получается требуемый результат. Под делимым ребенку нужно записать 10. Остатка у этого примера нет.

Предложите ребенку легкие примеры такого типа:

• 200 разделить на 20;
• 300 разделить на 30;
• 400 разделить на 40;
• 500 разделить на 50;
• 600 разделить на 60;
• 700 разделить на 70.

Далее можно переходить к сложным примерам. Но только после того, как ребенок усвоит результат.

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик

Как объяснить деление с остатком?

Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:

Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).

Обучение школьника должно проходить поэтапно, от простых примеров к более сложным.  Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.

Алгоритм действий при делении в столбик

Решая задание путем деления чисел в столбик эффективней использовать максимально простой метод:

1. Найти в выражении делимое и делитель.

2. Написать в примере делимое и под «уголок» делитель.

3. Установить ту часть делимого, которую можно использовать в первичном делении.

4. Установить количество раз которое делитель поместится в избранной части делимого.

5. Определить произведение делителя и полученного числа под уголком, результат записать под избранной частью делимого.

6. Найти остаток и продолжить осуществление действий до получения результат «0».

Вышеуказанный порядок выполнения операций будет далее рассмотрен на примере.

Пожелания к взрослым

Далеко не каждый педагог может похвастаться талантами Антона Макаренко и детей с врождёнными математическими способностями наблюдать приходится не часто. Поэтому задача близких для ребенка взрослых помочь преодолеть ему трудности в учебе.

Деление в столбик относиться к программе 2-3 классов средней школы. Конечно для многих взрослых это было давно и не правда. Однако помочь ребенку именно на азах и самому вспомнить те далекие годы и знания значительно легче, чем, когда дитя упустив азы и знания начальной школы столкнётся с настоящей абстрактной математикой. Тогда уже родителям «малой кровью» не отделаться и скорее всего без найма репетиторов не обойтись.

Поэтому своевременное постижение математики задача не только ребенка, но и заботливых близких, которые в силу возраста в состоянии предугадать динамику и развитие дальнейших событий в судьбе их любимого чада и внести соответствующие корректировки.

Статья составлена на основании учебников: «Математика 2 класс» Моро М.И. Бантова М.А. 1974, Математика. 3 класс. 2 часть — Аргинская И.И. 2014  и педагогической практики сотрудников ЧУ Детский дом «Солнышко» РК domsolnyshko.kz/o-nas/o-detskom-dome/.

Делим десятичные дроби на 1000, 100, 10: как это сделать правильно?

Исходя из имеющихся и известных правил деления так называемых «обыкновенных дробей», деление на числа с нулями равносильно умножению. Необходимо перенести запятую на нужное количество цифр. Если значений не хватает, нули просто добавляются. Это же происходит с бесконечными десятичными дробями.

Поэтому, чтобы верно произвести действие деления десятичной дроби на числа с нулями, нужно перенести запятую на столько цифр, сколько нулей стоит после единицы в делителе: если это число 10 – то нуль один, если 100 – то два. И так далее.

Делим десятичные дроби на 1000, 100, 10

Примеры с бесконечными дробями решаются также:

Делим десятичные дроби на 1000, 100, 10

Подготовка в обучению

Для того, чтобы начать объяснять ребенку принцип счета столбиком, Вы должны понять: готов ли он к этому. Обучение должно начинаться только в том случае, если малыш свободно и правильно производит простые арифметические действия с числами от 0 до 10.

Сюда входят сложение, вычитание, деление и умножение (если ребенок не знает одно из приведенных действий, то лучше научите его заранее, ведь «столбик» желательно учить комплексом, т.е. все вариации разбирать вместе)

Важно повторить все перед «стартом», ведь это — самая основа, которую закладывают во 2 — 3 классе.

Не забудьте «разобрать по полочкам» понятие единиц, десятков, сотен и тысяч! Без этого ребенок не сможет наиболее точно понять принцип подсчета и дальше двузначных чисел вы не уйдете.

Здесь отлично подойдет методика, где ученик записывает разные цифры числа под строкой своего разряда. Например: 2312 и 534 — тут получится, что 5 будет под 3, 3 под 1, а 4 под 2, двойка в разряде тысяч будет стоять одна, ведь тысячных частей больше нет.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

1. «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
2. «Деление. Уровень 4. Рабочая тетрадь» от Kumon
3. «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является  усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей

Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода

Для того чтобы легко научить ребёнка операции деления нужно:

• Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
• Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.

Деление столбиком с остатком

Пусть нам требуется разделить  1340  на  23.

Определяем неполное делимое — это число  134.  Записываем в частное  5  и из  134  вычитаем  115.  В остатке получилось  19:

Сносим следующую цифру делимого —  0.  Определяем, сколько раз  23  содержится в числе  190.  Получаем число  8,  записываем его в частное, а из  190  вычитаем  184.  Получаем остаток  6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное  58  и остаток  6:

1340 : 23 = 58 (остаток 6).

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить  3  на  10.  Мы видим, что  10  ни разу не содержится в числе  3,  поэтому записываем в частное  0  и из  3  вычитаем  0  (10 · 0 = 0).  Проводим горизонтальную черту и записываем остаток —  3:

3 : 10 = 0 (остаток 3).

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

• Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
• Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
• Запишите под числом 35 число 32.
• Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Деление с остатком

Простые примеры для ребенка

На этом же примере можно продолжить:

• При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
• При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
• Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
• В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
• При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.

Убедиться в том, что ребенок усвоил азы арифметики и правильно их понял

Иногда корень проблемы находится именно в этом. Базовыми основами для школьника являются понимание:

1. сложения;

2. вычитание;

3. таблицы умножения.

Взрослому обязательно надо напомнить ребенку основы умножения и убедиться в знании им таблицы. Также нужно быть уверенным в том, что ребенок знает разряды и классы чисел и не путается в сотнях, десятках, единицах и т.п. Знает ли и помнит ли он, что:

1. Числа – это единицы счета, с помощью которых можно посчитать все на Свете, а цифры – это специальные знаки, которыми их записывают.

2. Все многозначные числа разбиты на группы по три в каждой и эти группы зовут классами, — единицы, десятки, сотни и т.д. этого класса, т.е. единиц, десятков, сотен, тысяч, миллионов и т.п.

3. Все числа имеют разряд в зависимости, от той позиции которую они занимают в числе.

Если вместо этих арифметических азов наблюдается «провал» в фундаменте базовых математических знаний, на дальнейшие успехи в усвоении математики можно не рассчитывать. Математика относится к разряду точных наук и лежит в основе многих других дисциплин которые предстоит изучать школьнику.

Довести до ребенка мысль о том, что пробелов в ней быть не должно, — важная задача для взрослого. Если часть материала не была усвоена, по независящим от ученика обстоятельствам, например, при болезни, изучить, то, что давали на уроке необходимо самостоятельно дома. Делать это надо непременно, чтобы избежать затруднений при решении примеров и задач, как в самой математике, так и смежных с ней дисциплин, которые предстоят к изучению в будущем.

Как научиться делить столбиком трехзначные числа

Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.

Для примера рассмотрим следующие действия: 146676 : 719

146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.

1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».

Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.

Деление в столбик – правила

Для того, чтобы уметь делить в столбик необходимо знать некоторые правила. Именно об этом и пойдет далее речь. Ведь деление в столбик невозможно освоить если не знать элементарного – таблицы умножения. Считать простые примеры на умножение необходимо быстро и в уме. Это только в начале обычно дети пользуются черновиками, чтобы подобрать множитель, таким образом найти частное. Еще надобно уметь разбивать числа на сотни, десятки, тысячи – не путаться и в этих понятиях. Для наглядности, где делимое, где делитель, где частное можете изучить термины на изображении ниже.

Что нужно знать для деления в столбик?

Прежде, чем приступать к делению, следует проверить ребенка на знания элементарных правил. Ведь пропускать математику нельзя. А если пропуски все же были, то нужно изучить тот материал, что изучали ранее на уроках в школе

Понадобится обратить внимание на такие знания, как:

Запомнил ли школьник, как называются все элементы, участвующие в процессе деления.

Обратите внимание на знание таблицы умножения ребенком.
Еще ребенок должен усвоить, какие бывают разряды числа (единицы, десятки, сотни).

Пример: 

1. 57: 3, где 57 – это делимое, число, что разделяют на доли, а 3 – это делитель, указывающий, на сколько делить предыдущее число.
2. Определяемся, вначале какие единицы выделить в делимом для осуществления деления в столбик числа 57. Число 5 > 3.
3. Узнайте, сколько раз следует взять число 3, чтобы получить 5. Результат 3 · 1 = 3 ≤ 5. Значит подходит и 1 поставьте в качестве первой цифры частного.
4. Теперь вычитание: 5 — 3 = 2. Остаток 2 и единицу сносим, выходит 27.
5. Находим теперь, на какое число нужно умножить 3, чтобы результат был 27. Согласно таблице умножения 3 · 9 = 27.
6. Итого результат 19.

Умножение, деление – взаимосвязаны между собой, хотя и противоположные операции. Чтобы проверить, верно ли нашли частное, необходимо выполнить умножение. Потому таблица умножения и умение умножать на черновике без калькулятора всегда пригодится ребенку, также еще при умножении следует уметь правильно прибавлять, а при делении в столбик вычитать. В математики все действия с числами между собой взаимосвязаны.

Ниже смотрите пример деления в столбик 536 на 4. Действия с трехзначным делимым выполняются аналогично, что и с двухзначным.

Деление

Деление в школе начинают учить уже с третьего класса. Школьники только изучают азы процесса, выполняют самые простые примеры на это действие.

Примеры подобны умножению, только детей учат таблице деления, а не умножения. Школьники должны уловить саму суть, что означает поделить число на несколько частей, изучают, что такое делимое, делитель, частное. Узнают, как проверить умножением правильность решения примера или же задачи. В столбик дети еще не считают, так как даются самые простые примеры и все числа из таблицы умножения. Пример: 81 : 9 = 9.

Процесс деления в четвертом классе значительно усложняется. Детям дают вначале года вспомнить, что они учили в третьем классе, а далее уже начинают осваивать технику деления чисел в столбик. Именно за этот учебный год осваивают такие знания. Ниже приведен алгоритм решения примеров в столбик с подробным описанием процесса.

Здесь даже учтено то, что возможно будет остаток при делении, что число получится не цельным, а через запятую.

Как разделить десятичную дробь на натуральное число столбиком

Делить столбиком можно не только натуральные числа, но и дроби. Алгоритм мы подробно опишем здесь. Итак, как делить десятичные дроби на натуральные числа в столбик:

1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).

2. Выполнить деление по стандартной схеме. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.

Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться — получится периодическая дробь.

Пример: Разделить столбиком 49,14÷3

Как решаем 1. Делим столбиком, предварительно дописав два нуля к десятичной дроби. 2. После того, как мы поделили целую часть дроби и получили 16, отделяем ответ запятой (16) и продолжаем деление уже для дробной части В конце у нас нулевой остаток, значит деление завершено.

Ответ: 49,14÷3 = 16,38

Признаки делимости

Для разбора алгоритма деления 2 значений, которые являются внетабличными (отсутствуют в таблице умножения), необходимо обозначить элементы операции. Пусть дано некоторое выражение v: t = p. Коэффициенты в нем расшифровываются следующим образом:

1. V — делимое, т. е. число, которое требуется разделить.
2. T — математики называют его делителем.
3. P — частное является числовым результатом, который будет получаться при делении двух величин.

Иногда в литературе с физико-математическим уклоном можно встретить такую запись: v / t = p. Кроме того, числа классифицируются на простые и составные. К первой группе относятся все значения, которые делятся без остатка только на 1 или на значение равное исходному, т. е. 23 делится на 1 и на 23, а остальных делителей у него нет вообще. Вторая группа — значения, состоящие из нескольких множителей. Например, 100 = 25 * 4 = 5 * 5 * 2 * 2.

Десятичная система состоит из однозначных цифр, формирующих двузначные, трехзначные, четырехзначные, пятизначные числа (количество разрядов можно продолжать до бесконечности). Для деления двухзначного значения на однозначное без остатка необходимо знать следующие свойства (признаки деления):

1. 0: операция невозможна, поскольку превращает все выражение в пустое множество.
2. 1: делятся все значения.
3. 2: последняя цифра является четным значением, т. е. 0, 2, 4, 6 и 8.
4. 3: сумму цифр, составляющих число, можно разделить на 3. Например, проверить возможность деления 72 на 3. Для этого следует применить такое правило: 7 + 2 = 9. По таблице умножения 9 делится на 3 без остатка. Следовательно, 72 делится на 3.
5. 4: сумма двух цифр делится на 4. Если представлено 5-значное число, то нужно рассматривать 2 последних цифры.
6. 5: последней цифрой является 0 или 5.
7. 6: деление на составные части, т. е. на 2 и 3.
8. 7: возможность выполнения операции определяется по формуле / 7, где а, b и с — соответствуют первой, второй и третьей цифрам. Для двузначной величины — a / 7 и b / 7.
9. 8: должно делиться на 2 и 4. Если количество цифр больше 2, то следует рассматривать делимость без остатка трех последних цифр.
10. 9: деление по таблице умножения. Если число состоит из трех и более цифр, то следует рассматривать деления их суммы на 9.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

рисунок из презентации на тему деления трёхзначного числа столбиком

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

пример деления трехзначного числа на однозначное столбиком

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

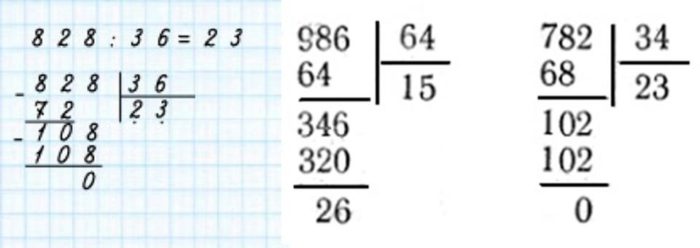
примеры деления столбиком трехзначных чисел на двузначные

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

пример деления в столбик трёхзначного числа на трёхзначное с остатком